Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T17:31:38.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Semimartingale decomposition of convex functions of continuoussemimartingales by Brownian perturbation

Published online by Cambridge University Press:  17 May 2013

Nastasiya F. Grinberg
Nastasiya F. Grinberg*
Affiliation:
Department of Statistics, University of Warwick, Coventry, CV4 7AL, UK. [email protected]
Get access

Abstract

In this note we prove that the local martingale part of a convex functionf of a d-dimensional semimartingaleX = M + A can be written in terms ofan Itô stochastic integral∫H(X)dM, whereH(x) is some particular measurable choice ofsubgradient \hbox{$\sub$}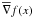∇f(x) off at x, and M is the martingale partof X. This result was first proved by Bouleau in [N. Bouleau, C.R. Acad. Sci. Paris Sér. I Math. 292 (1981) 87–90]. Here wepresent a new treatment of the problem. We first prove the result for\hbox{$\widetilde{X}=X+\epsilon B$}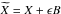􏽥X=X+ϵB,ϵ > 0, where B is a standardBrownian motion, and then pass to the limit as ϵ → 0, using results in[M.T. Barlow and P. Protter, On convergence of semimartingales. In Séminaire deProbabilités, XXIV, 1988/89, Lect. Notes Math., vol. 1426.Springer, Berlin (1990) 188–193; E. Carlen and P. Protter, Illinois J. Math.36 (1992) 420–427]. The former paper concerns convergence ofsemimartingale decompositions of semimartingales, while the latter studies a special caseof converging convex functions of semimartingales.

Keywords

Itô’s lemmacontinuous semimartingalesconvex functions.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 17 , 2013 , pp. 293 - 306
Copyright
© EDP Sciences, SMAI, 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M.T. Barlow and P. Protter, On convergence of semimartingales. In Séminaire de Probabilités, XXIV, 1988/89, Lect. Notes Math., vol. 1426. Springer, Berlin (1990) 188–193.
Bouleau, N., Semi-martingales à valeurs Rd et fonctions convexes. C. R. Acad. Sci. Paris Sér. I Math. 292 (1981) 87–90. Google Scholar
Bouleau, N., Formules de changement de variables. Ann. Inst. Henri Poincaré Probab. Statist. 20 (1984) 133–145. Google Scholar
Carlen, E. and Protter, P., On semimartingale decompositions of convex functions of semimartingales. Illinois J. Math. 36 (1992) 420–427. Google Scholar
Cranston, M., Kendall, W.S. and March, P., The radial part of Brownian motion. II. Its life and times on the cut locus. Probab. Theory Relat. Fields 96 (1993) 353–368. Google Scholar
Föllmer, H. and Protter, P., On Itô’s formula for multidimensional Brownian motion. Probab. Theory Relat. Fields 116 (2000) 1–20. Google Scholar
Föllmer, H., Protter, P. and Shiryayev, A.N., Quadratic covariation and an extension of Itô’s formula. Bernoulli 1 (1995) 149–169. Google Scholar
Fuhrman, M. and Tessitore, G., Generalized directional gradients, backward stochastic differential equations and mild solutions of semilinear parabolic equations. Appl. Math. Optim. 51 (2005) 279–332. Google Scholar
J.R. Giles, Convex analysis with application in the differentiation of convex functions, Research Notes Math., vol. 58. Pitman (Advanced Publishing Program), Boston, Mass (1982).
Kendall, W.S., The radial part of Brownian motion on a manifold: a semimartingale property. Ann. Probab. 15 (1987) 1491–1500. Google Scholar
P.-A. Meyer, Un cours sur les intégrales stochastiques. In Séminaire de Probabilités, X (Seconde partie: Théorie des intégrales stochastiques, Univ. Strasbourg, Strasbourg, année universitaire 1974/1975), Lecture Notes Math., vol. 511. Springer, Berlin (1976) 245–400.
D. Revuz and M. Yor, Continuous martingales and Brownian motion, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 293, 3th edition. Springer-Verlag, Berlin (1999).
R.T. Rockafellar, Convex analysis. Princeton Mathematical Series, No. 28. Princeton University Press, Princeton, N.J. (1970).
Russo, F. and Vallois, P., The generalized covariation process and Itô formula. Stochastic Process. Appl. 59 (1995) 81–104. Google Scholar
Russo, F. and Vallois, P., Itô formula for C 1-functions of semimartingales. Probab. Theory Relat. Fields 104 (1996) 27–41. Google Scholar