Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wu, Qiang
Ying, Yiming
and
Zhou, Ding-Xuan
2006.
Topics in Multivariate Approximation and Interpolation.
Vol. 12,
Issue. ,
p.
257.
Florko, B. V.
and
Korogodina, V. L.
2007.
Analysis of the distribution structure as exemplified by one cytogenetic problem.
Physics of Particles and Nuclei Letters,
Vol. 4,
Issue. 4,
p.
331.
Wu, Qiang
Ying, Yiming
and
Zhou, Ding-Xuan
2007.
Multi-kernel regularized classifiers.
Journal of Complexity,
Vol. 23,
Issue. 1,
p.
108.
Klemelä, Jussi
2007.
Density estimation with stagewise optimization of the empirical risk.
Machine Learning,
Vol. 67,
Issue. 3,
p.
169.
Nandakumar, K.
Yi Chen
Dass, S.C.
and
Jain, A.K.
2008.
Likelihood Ratio-Based Biometric Score Fusion.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
Vol. 30,
Issue. 2,
p.
342.
Barron, Andrew R.
Cong Huang
Li, Jonathan Q.
and
Xi Luo
2008.
MDL, penalized likelihood, and statistical risk.
p.
247.
2009.
Smoothing of Multivariate Data.
p.
575.
Raghavendra, R
Ashok, Rao
and
Hemantha Kumar, G
2010.
Multimodal Biometric Score Fusion Using Gaussian Mixture Model and Monte Carlo Method.
Journal of Computer Science and Technology,
Vol. 25,
Issue. 4,
p.
771.
Sriperumbudur, Bharath K.
2011.
Mixture density estimation via Hilbert space embedding of measures.
p.
1027.
Nanni, Loris
Lumini, Alessandra
and
Brahnam, Sheryl
2011.
Likelihood ratio based features for a trained biometric score fusion.
Expert Systems with Applications,
Vol. 38,
Issue. 1,
p.
58.
Oreshkin, Boris N.
and
Coates, Mark J.
2011.
Analysis of error propagation in particle filters with approximation.
The Annals of Applied Probability,
Vol. 21,
Issue. 6,
Korogodina, V. L.
Florko, B. V.
and
Osipova, L. P.
2012.
Radiobiology and Environmental Security.
p.
163.
Tyagi, Vivek
Kalyanaraman, Shivkumar
and
Krishnapuram, Raghuram
2012.
Vehicular Traffic Density State Estimation Based on Cumulative Road Acoustics.
IEEE Transactions on Intelligent Transportation Systems,
Vol. 13,
Issue. 3,
p.
1156.
Korogodina, Victoria L.
Florko, Boris V.
and
Osipova, Ludmila P.
2013.
Radiation-Induced Processes of Adaptation.
p.
151.
Sun, Hong Wei
and
Liu, Ping
2013.
The optimal solution of multi-kernel regularization learning.
Acta Mathematica Sinica, English Series,
Vol. 29,
Issue. 8,
p.
1607.
Sancetta, Alessio
2013.
A Recursive Algorithm for Mixture of Densities Estimation.
IEEE Transactions on Information Theory,
Vol. 59,
Issue. 10,
p.
6893.
Wang, Shaojun
Greiner, Russell
and
Wang, Shaomin
2013.
Consistency and Generalization Bounds for Maximum Entropy Density Estimation.
Entropy,
Vol. 15,
Issue. 12,
p.
5439.
Xu, Yong
and
Lu, Yuwu
2015.
Adaptive weighted fusion: A novel fusion approach for image classification.
Neurocomputing,
Vol. 168,
Issue. ,
p.
566.
Sancetta, Alessio
2016.
Greedy algorithms for prediction.
Bernoulli,
Vol. 22,
Issue. 2,
Tran, Quang Duc
and
Liatsis, Panos
2016.
RABOC: An approach to handle class imbalance in multimodal biometric authentication.
Neurocomputing,
Vol. 188,
Issue. ,
p.
167.
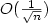 bound on the estimation errorwhich does not depend on the number of densities in the estimatedcombination. Under the boundedness assumption,this improves the bound of Li and Barron by removing the $\log n$
bound on the estimation errorwhich does not depend on the number of densities in the estimatedcombination. Under the boundedness assumption,this improves the bound of Li and Barron by removing the $\log n$ 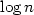 factor and also generalizes it to the base classes with convergingDudley integral.
factor and also generalizes it to the base classes with convergingDudley integral.

