Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T04:52:08.240Z Has data issue: false hasContentIssue false
  • English
  • Français

The large deviation principle for certain series

Published online by Cambridge University Press:  15 September 2004

Miguel A. Arcones
Miguel A. Arcones*
Affiliation:
Department of Mathematical Sciences, Binghamton University, Binghamton, NY 13902, USA; [email protected].
Get access

Abstract

We study the large deviation principle for stochastic processes of the form $\{\sum_{k=1}^{\infty}x_{k}(t)\xi_{k}:t\in T\}$ 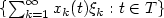, where $\{\xi_{k}\}_{k=1}^{\infty}$ 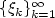is a sequence of i.i.d.r.v.'s with mean zero and $x_{k}(t)\in \mathbb{R}$ 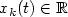. We present necessary and sufficient conditions for the large deviation principle for these stochastic processes in several situations. Our approach is based in showing the large deviation principle of the finite dimensional distributions and an exponential asymptotic equicontinuity condition. In order to get the exponential asymptotic equicontinuity condition, we derive new concentration inequalities, which are of independent interest.

Keywords

Large deviationsstochastic processes.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 8 , August 2004 , pp. 200 - 220
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arcones, M.A., The large deviation principle for stochastic processes I. Theor. Probab. Appl. 47 (2003) 567–583. CrossRef
Arcones, M.A., The large deviation principle for stochastic processes. II. Theor. Probab. Appl. 48 (2004) 19–44. CrossRef
Baxter, J.R. and Naresh, C.J., An approximation condition for large deviations and some applications, in Convergence in ergodic theory and probability (Columbus, OH, 1993), de Gruyter, Berlin. Ohio State Univ. Math. Res. Inst. Publ. 5 (1996) 63–90.
N.H. Bingham, C.M. Goldie and J.L. Teugels, Regular Variation. Cambridge University Press, Cambridge, UK (1987).
Y.S. Chow and H. Teicher, Probability Theory. Independence, Interchangeability, Martingales. Springer-Verlag, New York (1978).
A. Dembo and O. Zeitouni, Large Deviations Techniques and Applications. Springer, New York (1998).
J.D. Deuschel and D.W. Stroock, Large Deviations. Academic Press, Inc., Boston, MA (1989).
Gluskin, E.D. and Kwapień, S., Tail and moment estimates for sums of independent random variables with logarithmically concave tails. Studia Math. 114 (1995) 303–309.
Hitczenko, P., Montgomery-Smith, S.J. and Oleszkiewicz, K., Moment inequalities for sums of certain independent symmetric random variables. Studia Math. 123 (1997) 15–42.
S. Kwapień and W.A. Woyczyński, Random Series and Stochastic Integrals: Single and Multiple. Birkhäuser, Boston (1992).
Latala, R., Tail and moment estimates for sums of independent random vectors with logarithmically concave tails. Studia Math. 118 (1996) 301–304.
M. Ledoux and M. Talagrand, Probability in Banach Spaces. Springer-Verlag, New York (1991).
M. Ledoux, The Concentration of Measure Phenomenon. American Mathematical Society, Providence, Rhode Island (2001).
Lynch, J. and Sethuraman, J., Large deviations for processes with independent increments. Ann. Probab. 15 (1987) 610–627. CrossRef
Talagrand, M., A new isoperimetric inequality and the concentration of measure phenomenon. Geometric aspects of functional analysis (1989–90), Springer, Berlin. Lect. Notes Math. 1469 (1991) 94–124. CrossRef
Talagrand, M., The supremum of some canonical processes. Amer. J. Math. 116 (1994) 283–325. CrossRef
Varadhan, S.R.S., Asymptotic probabilities and differential equations. Comm. Pures App. Math. 19 (1966) 261–286. CrossRef