Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T18:06:27.396Z Has data issue: false hasContentIssue false
  • English
  • Français

Histogram selection in non Gaussian regression

Published online by Cambridge University Press:  26 March 2009

Marie Sauvé
Marie Sauvé*
Affiliation:
Laboratoire de mathématiques – Bâtiment 425, Université Paris Sud, 91405 Orsay Cedex, France; [email protected]
Get access

Abstract

We deal with the problem of choosing a piecewise constant estimator of a regression function s mapping $\mathcal{X}$ 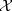into $\mathbb{R}$ 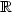.We consider a non Gaussian regression framework with deterministic design points, and we adopt the non asymptotic approach of model selection via penalization developed by Birgé and Massart. Given a collection of partitions of $\mathcal{X}$ 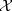, with possibly exponential complexity,and the corresponding collection of piecewise constant estimators, we propose a penalized least squares criterion which selects a partition whose associated estimator performs approximately as well as the best one, in the sense that its quadratic risk is close to the infimum of the risks. The risk bound we provide is non asymptotic.

Keywords

CARTchange-points detectiondeviation inequalitiesmodel selectionoracle inequalitiesregression
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 13 , July 2009 , pp. 70 - 86
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baraud, Y., Model selection for regression on a fixed design. Probab. Theory Related Fields 117 (2000) 467–493. CrossRef
Baraud, Y., Comte, F. and Viennet, G., Model Selection for (auto-)regression with dependent data. ESAIM: PS 5 (2001) 33–49. CrossRef
Birgé, L. and Massart, P., Gaussian model selection. J. Eur. Math. Soc. 3 (2001) 203–268.
L. Birgé and P. Massart, Minimal penalties for gaussian model selection. To be published in Probab. Theory Related Fields (2005).
Birgé, L. and Rozenholc, Y., How many bins should be put in a regular histogram. ESAIM: PS 10 (2006) 24–45. CrossRef
Bousquet, O., Concentration Inequalities for Sub-Additive Functions Using the Entropy Method. Stochastic Inequalities and Applications 56 (2003) 213–247. CrossRef
L. Breiman, J. Friedman, R. Olshen and C. Stone, Classification And Regression Trees. Chapman et Hall (1984).
Castellan, G., Modified Akaike's criterion for histogram density estimation. C.R. Acad. Sci. Paris Sér. I Math. 330 (2000) 729–732. CrossRef
O. Catoni, Universal aggregation rules with sharp oracle inequalities. Ann. Stat. (1999) 1–37.
E. Lebarbier, Quelques approches pour la détection de ruptures à horizon fini. Ph.D. thesis, Université Paris XI Orsay (2002).
Lugosi, G. and Nobel, A., Consistency of data-driven histogram methods for density estimation and classification. Ann. Stat. 24 (1996) 786–706.
Mallows, C.L., Some comments on c p . Technometrics 15 (1973) 661–675.
P. Massart, Notes de Saint-Flour. Lecture Notes to be published (2003).
Nobel, A., Histogram regression estimation using data-dependent partitions. Ann. Stat. 24 (1996) 1084–1105.
M. Sauvé, Sélection de modèles en régression non gaussienne. Applications à la sélection de variables et aux tests de survie accélérés. Ph.D. thesis, Université Paris XI Orsay (2006).
M. Sauvé and C. Tuleau, Variable selection through CART. Research Report 5912, INRIA (2006).