Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T22:41:48.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusions with measurement errors.I. Local Asymptotic Normality

Published online by Cambridge University Press:  15 August 2002

Arnaud Gloter  and
Jean Jacod
Arnaud Gloter
Affiliation:
G.R.A.P.E., UMR 5113 du CNRS, Université Montesquieu (Bordeaux), Avenue Léon Duguit, 33608 Pessac, France; [email protected].
Jean Jacod
Affiliation:
Laboratoire de Probabilités et Modèles Aléatoires, UMR 7599 du CNRS, Université Paris 6, 4 place Jussieu, 75252 Paris, France; [email protected].
Get access

Abstract

We consider a diffusion process X which is observed at times i/nfor i = 0,1,...,n, each observation being subject to a measurementerror. All errors are independent and centered Gaussian with knownvariance pn . There is an unknown parameter within the diffusioncoefficient, to be estimated. In this first paper thecase when X is indeed a Gaussian martingale is examined: we can provethat the LAN property holds under quite weak smoothness assumptions,with an explicit limiting Fisher information. 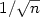What is perhaps the mostinteresting is the rate at which this convergence takes place:it is $1/\sqrt{n}$ (as when there is no measurement error) when pn goes fastenough to 0, namely npn is bounded. Otherwise, and provided thesequence pn itself is bounded, the rate is (pn / n) 1/4. Inparticular if pn = p does not depend on n, we get a rate n -1/4.

Keywords

Statistics of diffusionsmeasurementerrorsLAN property.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 5 , 2001 , pp. 225 - 242
Copyright
© EDP Sciences, SMAI, 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bickel, P. and Ritov, Y., Inference in hidden Markov models. I. Local asymptotic normality in the stationary case. Bernoulli 2 (1996) 199-228. CrossRef
P. Bickel and Y. Ritov, Asymptotic normality for the maximum likelihood estimator for general hidden Markov models. Ann. Statist. 26 (1998) 1614-1635.
G. Dohnal, On estimating the diffusion coefficient. J. Appl. Probab. 24 (1987) 105-114.
V. Genon-Catalot and J. Jacod, On the estimation of the diffusion coefficient for multidimensional diffusion processes. Ann. Inst. H. Poincaré Probab. Statist. 29 (1993) 119-153.
V. Genon-Catalot and J. Jacod, Estimation of the diffusion coefficient for diffusion processes: random sampling. Scand. J. Statist. 21 (1994) 193-221.
A. Gloter and J. Jacod, Diffusion with measurement error. II. Optimal estimators (2000).
E. Gobet, LAMN property for elliptic diffusions (2000).
J. Jacod and A. Shiryaev, Limit Theorems for Stochastic Processes. Springer-Verlag, Berlin (1987).
Jensen, J.L. and Petersen, N., Asymptotic normality of the Maximum likelihood estimator in state space models. Ann. Statist. 27 (1999) 514-535.
Leroux, B., Maximum likelihood estimation for hidden Markov models. Stochastic Process. Appl. 40 (1992) 127-143. CrossRef
L. LeCam and G.L. Yang, Asymptotics in Statistics. Springer-Verlag, Berlin (1990).
M.B. Malyutov and O. Bayborodin, Fitting diffusion and trend in noise via Mercer expansion, in Proc. 7th Int. Conf. on Analytical and Stochastic Modeling Techniques. Hamburg (2000).
Consistent, T. Ryden and asymptotically normal estimators for hidden Markov models. Ann. Statist. 22 (1994) 1884-1895.