Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T19:59:13.540Z Has data issue: false hasContentIssue false
  • English
  • Français

SPDEs with coloured noise: Analytic and stochastic approaches

Published online by Cambridge University Press:  20 October 2006

Marco Ferrante  and
Marta Sanz-Solé
Marco Ferrante
Affiliation:
Dipartimento di Matematica, Università di Padova, Via Belzoni 7, 35131 Padova, Italy; [email protected]
Marta Sanz-Solé
Affiliation:
Facultat de Matemàtiques, Universitat de Barcelona, Gran Via 585, 08007 Barcelona, Spain; [email protected]
Get access

Abstract

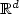We study strictly parabolic stochastic partial differential equations on $\mathbb{R}^d$ , d ≥ 1,driven by a Gaussian noise white in time and coloured in space. Assuming that thecoefficients of the differential operator are random, we give sufficient conditions on thecorrelation of the noise ensuring Hölder continuity for the trajectories of thesolution of the equation. For self-adjoint operators with deterministic coefficients, the mild and weakformulation of the equation are related, deriving path properties of the solution to aparabolic Cauchy problem in evolution form.


Keywords

Stochastic partial differential equationsmild and weak solutionsrandom noise.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 10 , February 2006 , pp. 380 - 405
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M. Abramowitz and I.A. Stegun, Handbook of mathematical functions. National Bureau of Standards (1964).
R.A. Adams, Sobolev spaces. Academic Press, New York-London (1975).
Alòs, E., León, J.A. and Nualart, D., Stochastic heat equation with random coefficients. Probab. Theory Related Fields 115 (1999) 41–94.
Dalang, R.C. and Frangos, N.E., The stochastic wave equation in two spatial dimensions. Ann. Probab. 26 (1998) 187–212.
Dalang, R.C., Extending the martingale measure stochastic integral with applications to spatially homogeneous s.p.d.e.'s. Electron. J. Probab. 4 (1999) 1–29. CrossRef
G. Da Prato and J. Zabczyk, Stochastic Equations in Infinite Dimensions, 2nd Edition. Cambridge University Press (1998).
W.F. Donoghue, Distributions and Fourier transforms. Academic Press, New York (1969).
S.D. Eidelman and N.V. Zhitarashu, Parabolic Boundary Value Problems. Birkhäuser Verlag, Basel (1998).
A. Friedman, Partial differential equations of parabolic type. Prentice-Hall, Inc., Englewood Cliffs, N.J. (1964).
I.M. Gel'fand and N.Ya. Vilenkin, Generalized functions. Vol. 4: Applications of harmonic analysis. Academic Press, New York (1964).
M.A Krasnoselskii, E.I. Pustylnik, P.E. Sobolevski and P.P. Zabrejko, Integral operators in spaces of summable functions. Noordhoff International Publishing, Leyden (1976).
A.A. Kirillov and A.D. Gvishiani, Theorems and problems in functional analysis. Springer-Verlag, New York-Berlin (1982).
Krylov, N.V. and Rozovsky, B.L., Stochastic evolution systems. Russian Math. Surveys 37 (1982) 81–105. CrossRef
Krylov, N.V., On Lp -theory of stochastic partial differential equations in the whole space. SIAM J. Math. Anal. 27 (1996) 313–340. CrossRef
N.V. Krylov, An analytic approach to SPDEs, in Stochastic partial differential equations: six perspectives, Math. Surveys Monogr. 64, American Mathematical Society, Providence (1999) 185–242.
Krylov, N.V. and Lototsky, V., Sobolev, A space theory of SPDEs with constant coefficients on a half line. SIAM J. Math. Anal. 30 (1998) 298–325. CrossRef
O.A. Ladyženskaja, V.A. Solonnikov and N.N. Ural'ceva, Linear and Quasilinear Equations of Parabolic Type. Translations of Mathematical Monographs 23, American Mathematical Society (1968).
O. Lévêque, Hyperbolic stochastic partial differential equations driven by boundary noises. Thèse 2452, Lausanne, EPFL (2001).
Mikulevicius, R., On the Cauchy problem for parabolic SPDEs in Hölder classes. Ann. Probab. 28 (2000) 74–103.
Pardoux, E., Stochastic partial differential equations and filtering of diffusion processes. Stochastics 3 (1979) 127–167. CrossRef
B.L. Rozovsky, Stochastic evolution equations. Linear theory and applications to non-linear filtering. Kluwer (1990).
L. Schwartz, Théorie des distributions. Hermann, Paris (1966).
Sanz-Solé, M. and Sarrà, M., Path properties of a class of Gaussian processes with applications to spde's. Canadian Mathematical Society Conference Proceedings 28 (2000) 303–316.
M. Sanz-Solé and M. Sarrà, Hölder Continuity for the stochastic heat equation with spatially correlated noise, in Progress in Probability 52, Birkhäuser Verlag (2002) 259–268.
Sanz-Solé, M. and Vuillermot, P.-A., Equivalence and Hölder-Sobolev regularity of solutions for a class of non-autonomous stochastic partial differential equations. Ann. Inst. H. Poincaré Probab. Statist. 39 (2003) 703–742. CrossRef
N. Shimakura, Partial differential operators of elliptic type. American Mathematical Society, Providence (1992).
H. Triebel, Theory of function spaces. II. Monographs in Mathematics 84, Birkhäuser Verlag, Basel (1992).
Walsh, J.B., Introduction, An to Stochastic Partial Differential Equations, in École d'été de Probabilités de Saint-Flour XIV (1984). Lect. Notes Math. 1180 (1986) 265–439. CrossRef