Surface energies in a two-dimensionalmass-spring model for crystals

Abstract

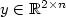We study an atomistic pair potential-energy E ⁽ⁿ⁾(y) that describesthe elastic behavior of two-dimensional crystals with n atoms where $y \in {\mathbb R}^{2\times n}$ characterizes the particle positions. The mainfocus is the asymptotic analysis of the ground state energy as ntends to infinity. We show in a suitable scaling regime where theenergy is essentially quadratic that the energy minimum of E ⁽ⁿ⁾admits an asymptotic expansion involving fractional powers of n:

${\rm min}_y E^{(n)}(y) = n \, E_{\mathrm{bulk}}+ \sqrt{n} \, E_\mathrm{surface} +o(\sqrt{n}), \qquad n \to \infty.$

The bulk energy density E _bulk is given by an explicitexpression involving the interaction potentials. The surface energyE _surface can be expressed as a surface integral where theintegrand depends only on the surface normal and the interactionpotentials. The evaluation of the integrand involves solving a discrete algebraic Riccati equation. Numerical simulations suggestthat the integrand is a continuous, but nowhere differentiable function ofthe surface normal.