Article contents
A singular perturbation problem in a systemof nonlinear Schrödinger equation occurring in Langmuir turbulence
Published online by Cambridge University Press: 15 April 2002
Abstract
The aim of this work is to establish, from amathematical point of view, the limit α → +∞ in the system $i \partial_t E+\nabla (\nabla . E)-\alpha^2 \nabla \times\nabla \times E =-|E|^{2\sigma}E,$ 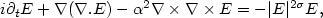 where $E:{\ensuremath{{\Bbb R}}}^3\rightarrow{\mathbb C}^3$
where $E:{\ensuremath{{\Bbb R}}}^3\rightarrow{\mathbb C}^3$ 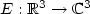 . This corresponds to an approximationwhich is made in the context of Langmuir turbulence in plasmaPhysics. The L 2-subcritical σ (that is σ ≤ 2/3)and the H 1-subcritical σ (that is σ ≤ 2) arestudied. In the physical case σ = 1, the limit is then studied for the $H^1({\ensuremath{{\Bbb R}}}^3)$
. This corresponds to an approximationwhich is made in the context of Langmuir turbulence in plasmaPhysics. The L 2-subcritical σ (that is σ ≤ 2/3)and the H 1-subcritical σ (that is σ ≤ 2) arestudied. In the physical case σ = 1, the limit is then studied for the $H^1({\ensuremath{{\Bbb R}}}^3)$ 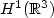 norm.
norm.
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 34 , Issue 1 , January 2000 , pp. 109 - 125
- Copyright
- © EDP Sciences, SMAI, 2000
References
- 5
- Cited by


