Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T21:24:44.296Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of the eikonal equation and shape from shading

Published online by Cambridge University Press:  15 April 2002

Ian Barnes  and
Kewei Zhang
Ian Barnes
Affiliation:
Department of Mathematics, Macquarie University, Sydney NSW 2109, Australia. ([email protected])
Kewei Zhang
Affiliation:
Department of Mathematics, Macquarie University, Sydney NSW 2109, Australia. ([email protected])
Get access

Abstract

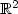In the shape from shading problem of computer vision oneattempts to recover the three-dimensional shape of an object orlandscape from the shading on a single image. Under theassumptions that the surface is dusty, distant, and illuminatedonly from above, the problem reduces to that of solving theeikonal equation |Du|=f on a domain in $\mathbb{R}^2$ . Despitevarious existence and uniqueness theorems for smooth solutions,we show that this problem is unstable, which is catastrophic forgeneral numerical algorithms.

Keywords

Eikonal equationshape from shadinginstabilitynumerical analysis.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 34 , Issue 1 , January 2000 , pp. 127 - 138
Copyright
© EDP Sciences, SMAI, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

R.A. Adams, Sobolev Space. Academic Press New York (1975).
J.M. Ball, A version of the fundamental theorem for Young measure. Lect. Notes Phys. Springer Verlag 344 (1988) 207-215.
Bruss, A.R., results applicable to computer vision. J. Math. Phys. 23 (1982) 890-896. CrossRef
J. Chabrowski and K.-W. Zhang, On shape from shading problem Functional Analysis, Approximation Theory and Numerical Analysis, J.M. Rassias Ed., World Scientific (1994) 93-105.
B. Dacorogna Direct Methods in the Calculus of Variations. Springer-Verlag (1989).
Deift, P. and Sylvester, J., Some remarks on the shape-from-shading problem in computer vision. J. Math. Anal. Appl. 84 (1981) 235-248. CrossRef
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions. Stud. in Adv. Math. CRC Press, Boca Raton (1992).
I. Ekeland and R. Temam, Analyse convexe et problèmes variationnels. Dunod Paris (1974).
L. Gritz, Blue Moon Rendering Tools: Ray tracing software available from ftp://ftp.gwu.edu/pub/graphics/BMRT (1995).
B.K.P. Horn, Robot Vision. Engineering and Computer Science Series, MIT Press, MacGraw Hill (1986).
B.K.P. Horn and M.J. Brooks, Shape from Shading. Ed. MIT Press Ser. in Artificial Intelligence (1989).
B.K.P. Horn and M.J. Brooks, Variational Approach to Shape from Shading in [11]
S. Levy, T. Munzner and M. Phillips, Geomview Visualisation software available from ftp.geom.umn.edu or http://www.geom.umn.edu/locate/geomview
Lions, P.-L., Rouy, E. and Tourin, A., Shape-from-shading, viscosity solutions and edges. Numer. Math. 64 (1993) 323-353. CrossRef
Pixar, The RenderMan Interface, version 3.1, official specification. Pixar (1989)
Phillips, M., Levy, S. and Munzner, T., Geomview: An Interactive Geometry Viewer. Notices Amer. Math. Soc. 40 (1993) 985-988.
Rouy, E. and Tourin, A., A viscosity solution approach to shape-from-shading. SIAM J. Numer. Anal. 29 (1992) 867-884. CrossRef
E.M. Stein, Singular Integrals and Differentiability Properties of Functions. Princeton University Press (1970).
L. Tartar, Compensated compactness and partial differential equations, in Microstructure and Phase Transitions, D. Kinderlehrer et al. Eds., Springer Verlag (1992).