Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T01:35:01.249Z Has data issue: false hasContentIssue false
  • English
  • Français

High order transmission conditions for thin conductive sheets in magneto-quasistatics

Published online by Cambridge University Press:  28 June 2011

Kersten Schmidt  and
Sébastien Tordeux
Kersten Schmidt
Affiliation:
Seminar for Applied Mathematics, ETH Zurich, 8092 Zurich, Switzerland, Project POEMS, INRIA Paris-Rocquencourt, 78153 Le Chesnay, France, currently at TU Berlin and DFG Research center , 10623 Berlin, Germany. [email protected]
Sébastien Tordeux
Affiliation:
Laboratoire de Mathématiques et de leurs Applications, UMR 5142, Université de Pau et des Pays de l'Adour, 64013 Pau, France, Project MAGIQUE-3D, INRIA Bordeaux-Sud-Ouest, 64013 Pau, France. [email protected]
Get access

Abstract

We propose transmission conditions of order 1, 2 and 3 approximating the shielding behaviour of thin conducting curved sheets for the magneto-quasistatic eddy current model in 2D. This model reduction applies to sheets whose thicknesses ε are at the order of the skin depth or essentially smaller. The sheet has itself not to be resolved, only its midline is represented by an interface. The computation is directly in one step with almost no additional cost. We prove the well-posedness w.r.t. 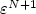to the small parameter ε and obtain optimal bound for the modelling error outside the sheet of order $\varepsilon^{N+1}$ for the condition of order N. We end the paper with numerical experiments involving high order finite elements for sheets with varying curvature.

Keywords

Asymptotic expansionstransmission conditionthin conducting sheets
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 45 , Issue 6 , November 2011 , pp. 1115 - 1140
Copyright
© EDP Sciences, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antoine, X., Barucq, H. and Vernhet, L., High-frequency asymptotic analysis of a dissipative transmission problem resulting in generalized impedance boundary conditions. Asymptot. Anal. 26 (2001) 257–283.
Bartoli, N. and Bendali, A., Robust and high-order effective boundary conditions for perfectly conducting scatterers coated by a thin dielectric layer. IMA J. Appl. Math. 67 (2002) 479–508. CrossRef
Bendali, A. and Lemrabet, K., The effect of a thin coating on the scattering of a time-harmonic wave for the Helmholtz equation. SIAM J. Appl. Math. 6 (1996) 1664–1693. CrossRef
Bendali, A. and Lemrabet, K., Asymptotic analysis of the scattering of a time-harmonic electromagnetic wave by a perfectly conducting metal coated with a thin dielectric shell. Asymptot. Anal. 57 (2008) 199–227.
A. Bossavit, Computational Electromagnetism. Variational Formulation, Complementarity, Edge Elements. No. 2 in Academic Press Electromagnetism Series. Academic Press, San Diego (1998).
D. Braess, Finite Elements: Theory, Fast Solvers, and Applications in Solid Mechanics, 3th edition. Cambridge University Press (2007).
H. Brezis, Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer-Verlag, New York (2010).
Caloz, G., Costabel, M., Dauge, M. and Vial, G., Asymptotic expansion of the solution of an interface problem in a polygonal domain with thin layer. Asymptot. Anal. 50 (2006) 121–173.
Concepts Development Team. Webpage of Numerical C++ Library Concepts 2. http://www.concepts.math.ethz.ch (2011).
Duruflé, M., Haddar, H. and Joly, P., Higher order generalized impedance boundary conditions in electromagnetic scattering problems. C.R. Phys. 7 (2006) 533–542. CrossRef
Frauenfelder, P. and Lage, C., Concepts – an object-oriented software package for partial differential equations. ESAIM: M2AN 36 (2002) 937–951. CrossRef
Haddar, H., Joly, P. and Nguyen, H.M., Generalized impedance boundary conditions for scattering by strongly absorbing obstacles: the scalar case. Math. Models Methods Appl. Sci. 15 (2005) 1273–1300. CrossRef
Haddar, H., Joly, P. and Nguyen, H.M., Generalized impedance boundary conditions for scattering by strongly absorbing obstacles: the case of Maxwell s equations. Math. Models Methods Appl. Sci. 18 (2008) 1787–1827. CrossRef
Igarashi, H., Kost, A. and Honma, T., A boundary element analysis of magnetic shielding for electron microscopes. Compel 17 (1998) 585–594. CrossRef
Joly, P. and Tordeux, S., Asymptotic analysis of an approximate model for time harmonic waves in media with thin slots. ESAIM: M2AN 40 (2006) 63–97. CrossRef
Krähenbühl, L. and Muller, D., Thin layers in electrial engineering. Example of shell models in analysing eddy-currents by boundary and finite element methods. IEEE Trans. Magn. 29 (1993) 1450–1455.
M.A. Leontovich, On approximate boundary conditions for electromagnetic fields on the surface of highly conducting bodies (in russian). Research in the propagation of radio waves. Moscow, Academy of Sciences (1948) 5–12.
W. McLean, Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press (2000).
Miri, A.M., Riegel, N.A. and Meinecke, C., FE calculation of transient eddy currents in thin conductive sheets using dynamic boundary conditions. Int. J. Numer. Model. 11 (1998) 307–316. 3.0.CO;2-J>CrossRef
Nakata, T., Takahashi, N., Fujiwara, K. and Shiraki, Y., 3D magnetic field analysis using special elements. IEEE Trans. Magn. 26 (1990) 2379–2381. CrossRef
V. Péron and C. Poignard, Approximate transmission conditions for time-harmonic Maxwell equations in a domain with thin layer. Research Report RR-6775, INRIA (2008).
R. Perrussel and C. Poignard, Asymptotic Transmission Conditions for Steady-State Potential in a High Contrast Medium. A Uniform Variational Formulation for Resistive Thin Layers. Research Report RR-7163, INRIA (2010).
K. Schmidt, High-order numerical modeling of highly conductive thin sheets. Ph.D. thesis, ETH Zürich (2008).
Schmidt, K. and Tordeux, S., Asymptotic modelling of conductive thin sheets. Z. Angew. Math. Phys. 61 (2010) 603–626. CrossRef
Schmidt, K., Sterz, O. and Hiptmair, R., Estimating the eddy-current modelling error. IEEE Trans. Magn. 44 (2008) 686–689. CrossRef
T. Senior and J. Volakis, Approximate Boundary Conditions in Electromagnetics. Institution of Electrical Engineers (1995).
A.N. Shchukin, Propagation of Radio Waves (in Russian). Svyazizdat, Moscow (1940).