Article contents
The change in electric potential due to lightning
Published online by Cambridge University Press: 04 July 2008
Abstract
The change in the electric potential due to lightning is evaluated.The potential along the lightning channel is a constant which isthe projection of the pre-flash potential along a piecewise harmoniceigenfunction which is constant along the lightning channel.The change in the potential outside the lightning channel is a harmonicfunction whose boundary conditionsare expressed in terms of the pre-flash potential andthe post-flash potential along the lightning channel.The expression for the lightning induced electric potential change isderived both for the continuous equations, and for a spatially discretizedformulation of the continuous equations.The results for the continuous equations are based on the properties ofthe eigenvalues and eigenfunctions of the following generalized eigenproblem:Find $u \in H_0^1 (\Omega)$ 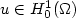 , $u \ne 0$
, $u \ne 0$ 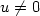 ,and $\lambda \in \mathbb{R}$
,and $\lambda \in \mathbb{R}$ 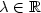 such that $\langle \nabla u, \nabla v \rangle_{\mathcal{L}} =\lambda \langle \nabla u, \nabla v \rangle_{\Omega}$
such that $\langle \nabla u, \nabla v \rangle_{\mathcal{L}} =\lambda \langle \nabla u, \nabla v \rangle_{\Omega}$ 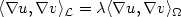 for all $v \in H_0^1 (\Omega)$
for all $v \in H_0^1 (\Omega)$ 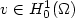 , where $\Omega \subset \mathbb{R}^n$
, where $\Omega \subset \mathbb{R}^n$  is a bounded domain (a box containing the thunderstorm), $\mathcal{L}$
is a bounded domain (a box containing the thunderstorm), $\mathcal{L}$ 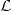 is a subdomain (the lightning channel),and $\langle \cdot, \cdot \rangle_{\Omega}$
is a subdomain (the lightning channel),and $\langle \cdot, \cdot \rangle_{\Omega}$ 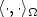 isthe inner product $\langle \nabla u,\nabla v\rangle_\Omega =\int_{\Omega}\nabla u\cdot\nabla v \; {{\rm d}x}.$
isthe inner product $\langle \nabla u,\nabla v\rangle_\Omega =\int_{\Omega}\nabla u\cdot\nabla v \; {{\rm d}x}.$ 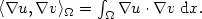
Keywords
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 42 , Issue 5 , September 2008 , pp. 887 - 901
- Copyright
- © EDP Sciences, SMAI, 2008
References
- 2
- Cited by


