Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T10:32:09.882Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary layer analysis and quasi-neutral limitsin the drift-diffusion equations

Published online by Cambridge University Press:  15 April 2002

Yue-Jun Peng
Yue-Jun Peng*
Affiliation:
Laboratoire de Mathématiques Appliquées, CNRS UMR 6620, Université Blaise Pascal (Clermont-Ferrand 2), 63177 Aubière Cedex, France, and, The Institute of Mathematical Sciences, The Chinese University of Hong Kong, Shatin NT, Hong Kong.
Get access

Abstract

We deal with boundary layers and quasi-neutral limits in the drift-diffusion equations. We first show that this limit is unique and determined by a system of two decoupled equations with given initial and boundary conditions. Then we establish the boundary layer equations and prove the existence and uniqueness of solutions with exponential decay. This yields a globally strong convergence (with respect to the domain) of the sequence of solutions and an optimal convergence rate $O(\varepsilon^\frac{1}{2})$ 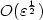to the quasi-neutral limit in L 2.

Keywords

Asymptotic analysisboundary layersoptimal convergence ratedrift-diffusion equations.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 35 , Issue 2 , March 2001 , pp. 295 - 312
Copyright
© EDP Sciences, SMAI, 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubin, J.P., Un théorème de compacité. C. R. Acad. Sci. Paris 256 (1963) 5042-5044.
Brenier, Y., Convergence of the Vlasov-Poisson system to the incompressible Euler equations. Comm. Partial Differential Equations 25 (2000) 737-754. CrossRef
Brézis, H., Golse, F., Sentis, R., Analyse asymptotique de l'équation de Poisson couplée à la relation de Boltzmann. Quasi-neutralité des plasmas. C. R. Acad. Sci. Paris 321 (1995) 953-959.
Cordier, S., Degond, P., Markowich, P., Schmeiser, C., Traveling wave analysis and jump relations for Euler-Poisson model in the quasineutral limit. Asymptot. Anal. 11 (1995) 209-224.
Cordier, S., Grenier, E., Quasineutral limit of an Euler-Poisson system arising from plasma physics. Comm. Partial Differential Equations 25 (2000) 1099-1113. CrossRef
Fife, P.C., Semilinear elliptic boundary value problems with small parameters. Arch. Rational Mech. Anal. 52 (1973) 205-232. CrossRef
Gajewski, H., On the uniqueness of solutions to the drift-diffusion model of semiconductor devices. Math. Models Methods Appl. Sci. 4 (1994) 121-133. CrossRef
I. Gasser, The initial time layer problem and the quasi-neutral limit in a nonlinear drift diffusion model for semiconductors. Nonlinear Differential Equations Appl. (to appear).
I. Gasser, D. Levermore, P. Markowich, C. Schmeiser, The initial time layer problem and the quasi-neutral limit in the drift-diffusion model (submitted).
Jüngel, A., A nonlinear drift-diffusion system with electric convection arising in semiconductor and electrophoretic modeling. Math. Nachr. 185 (1997) 85-110. CrossRef
Jüngel, A., Peng, Y.J., A hierarchy of hydrodynamic models for plasmas. Zero-relaxation-time limits. Comm. Partial Differential Equations 24 (1999) 1007-1033. CrossRef
A. Jüngel, Y.J. Peng, A hierarchy of hydrodynamic models for plasmas. Zero-electron-mass limits in the drift-diffusion equations. Ann. Inst. H. Poincaré, Anal. Non Linéaire 17 (2000) 83-118.
Jüngel, A., Peng, Y.J., Zero-relaxation-time limits in hydrodynamic models for plasmas revisited. Z. Angew. Math. Phys. 51 (2000) 385-396. CrossRef
A. Jüngel, Y.J. Peng, A hierarchy of hydrodynamic models for plasmas. Quasi-neutral limits in the drift-diffusion equations. Asymptot. Anal. (to appear).
J.L. Lions, Quelques méthodes de résolution des problèmes aux limites non linéaires. Dunod-Gauthier-Villard, Paris (1969).
Markowich, P.A., A singular perturbation analysis of the fundamental semiconductor device equations. SIAM J. Appl. Math. 44 (1984) 896-928. CrossRef
Markowich, P.A., Ringhofer, C., Schmeiser, C., An asymptotic analysis of one-dimensional models for semiconductor devices. IMA J. Appl. Math. 37 (1986) 1-24. CrossRef
Y.J. Peng, Convergence of the fractional step Lax-Friedrichs scheme and Godunov scheme for a nonlinear Euler-Poisson system. Nonlinear Anal. TMA 42 (2000) 1033-1054.
P. Raviart, On singular perturbation problems for the nonlinear Poisson equation or: A mathematical approach to electrostatic sheaths and plasma erosion, Lect. Notes of the Summer school in Ile d'Oléron, France (1997) 452-539.
L. Tartar, Compensated compactness and applications to partial differential equations. In: Nonlinear analysis and mechanics: Heriot-Watt Symp. Vol. 4 and Res. Notes Math. 3 (1979) 136-212.
Visintin, A., Strong convergence results related to strict convexity. Comm. Partial Differential Equations 9 (1984) 439-466. CrossRef