Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T05:28:57.982Z Has data issue: false hasContentIssue false
  • English
  • Français

Best N-term approximation in electronic structure calculations I.One-electron reduced density matrix

Published online by Cambridge University Press:  23 February 2006

Heinz-Jürgen Flad ,
Wolfgang Hackbusch  and
Reinhold Schneider
Heinz-Jürgen Flad
Affiliation:
Max-Planck-Institut für Mathematik in den Naturwissenschaften, Inselstr. 22-26, 04103 Leipzig, Germany. [email protected]; [email protected]
Wolfgang Hackbusch
Affiliation:
Max-Planck-Institut für Mathematik in den Naturwissenschaften, Inselstr. 22-26, 04103 Leipzig, Germany. [email protected]; [email protected]
Reinhold Schneider
Affiliation:
Christian-Albrechts-Universität Kiel, Christian-Albrechts-Platz 4, 24098 Kiel, Germany. [email protected]
Get access

Abstract

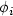We discuss best N-term approximation spaces for one-electron wavefunctions $\phi_i$ and reduced density matrices ρemerging from Hartree-Fock and density functional theory. The approximation spaces $A^\alpha_q(H^1)$ 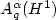for anisotropicwavelet tensor product bases have been recently characterized by Nitsche in terms of tensor product Besov spaces. We have used the norm equivalence of these spaces to weighted $\ell_q$ 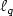spaces of wavelet coefficients toproof that both $\phi_i$ 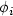and ρ are in $A^\alpha_q(H^1)$ 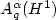for all $\alpha > 0$ 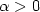with $\alpha = \frac{1}{q} - \frac{1}{2}$ 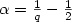. Our proof is based on the assumption that the $\phi_i$ 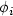possess an asymptotic smoothness property at the electron-nuclear cusps.

Keywords

Best N-term approximationwaveletsHartree-Fock methoddensity functional theory.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 40 , Issue 1 , January 2006 , pp. 49 - 61
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Braess, D., Asymptotics for the approximation of wave functions by exponential sums. J. Approx. Theory 83 (1995) 93–103. CrossRef
Bungartz, H.-J. and Griebel, M., Sparse grids. Acta Numerica 13 (2004) 147–269. CrossRef
Cohen, A., DeVore, R.A. and Hochmuth, R., Restricted nonlinear approximation. Constr. Approx. 16 (2000) 85–113. CrossRef
DeVore, R.A., Nonlinear approximation. Acta Numerica 7 (1998) 51–150. CrossRef
DeVore, R.A., Jawerth, B. and Popov, V., Compression of wavelet decompositions. Amer. J. Math. 114 (1992) 737–785. CrossRef
DeVore, R.A., Konyagin, S.V. and Temlyakov, V.N., Hyperbolic wavelet approximation. Constr. Approx. 14 (1998) 1–26. CrossRef
Flad, H.-J., Hackbusch, W., Kolb, D. and Schneider, R., Wavelet approximation of correlated wavefunctions. I. Basics. J. Chem. Phys. 116 (2002) 9641–9657. CrossRef
Flad, H.-J., Hackbusch, W., Luo, H. and Kolb, D., Diagrammatic multiresolution analysis for electron correlations. Phys. Rev. B. 71 (2005) 125115. CrossRef
Flad, H.-J., Hackbusch, W., Luo, H. and Kolb, D., Wavelet approach to quasi two-dimensional extended many-particle systems. I. supercell Hartree-Fock method. J. Comp. Phys. 205 (2005) 540–566. CrossRef
Fournais, S., Hoffmann-Ostenhof, M., Hoffmann-Ostenhof, T. and Ostergaard, T. S orensen, On the regularity of the density of electronic wavefunctions. Contemp. Math. 307 (2002) 143–148. CrossRef
Fournais, S., Hoffmann-Ostenhof, M., Hoffmann-Ostenhof, T. and Ostergaard, T. S orensen, The electron density is smooth away from the nuclei. Commun. Math. Phys. 228 (2002) 401–415. CrossRef
Garcke, J. and Griebel, M., On the computation of the eigenproblems of hydrogen and helium in strong magnetic and electric fields with the sparse grid combination technique. J. Comp. Phys. 165 (2000) 694–716. CrossRef
Halkier, A., Helgaker, T., Jørgensen, P., Klopper, W. and Olsen, J., Basis-set convergence of the energy in molecular Hartree-Fock calculations. Chem. Phys. Lett. 302 (1999) 437–446. CrossRef
Harrison, R.J., Fann, G.I., Yanai, T., Gan, Z. and Beylkin, G., Multiresolution quantum chemistry: Basic theory and initial applications. J. Chem. Phys. 121 (2004) 11587–11598. CrossRef
T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, Wiley, New York (1999).
Hill, R.N., Rates of convergence and error estimation formulas for the Rayleigh-Ritz variational method. J. Chem. Phys. 83 (1985) 1173–1196. CrossRef
M. Hoffmann-Ostenhof and R. Seiler, Cusp conditions for eigenfunctions of n-electron systems, Phys. Rev. A 23 (1981) 21–23.
Hoffmann-Ostenhof, M., Hoffmann-Ostenhof, T. and Stremnitzer, H., Local properties of Coulombic wave functions. Commun. Math. Phys. 163 (1994) 185–215. CrossRef
Hoffmann-Ostenhof, M., Hoffmann-Ostenhof, T. and Ostergaard, T. S orensen, Electron wavefunctions and densities for atoms. Ann. Henri Poincaré 2 (2001) 77–100. CrossRef
Kato, T., On the eigenfunctions of many-particle systems in quantum mechanics. Commun. Pure Appl. Math. 10 (1957) 151–177. CrossRef
Kutzelnigg, W., Theory of the expansion of wave functions in a Gaussian basis. Int. J. Quantum Chem. 51 (1994) 447–463. CrossRef
Kutzelnigg, W. and Morgan III, J.D., Rates of convergence of the partial-wave expansions of atomic correlation energies. J. Chem. Phys. 96 (1992) 4484–4508. CrossRef
Lieb, E.H. and Simon, B., The Hartree-Fock theory for Coulomb systems. Commun. Math. Phys. 53 (1977) 185–194. CrossRef
Luo, H., Kolb, D., Flad, H.-J., Hackbusch, W. and Koprucki, T., Wavelet approximation of correlated wavefunctions. II. Hyperbolic wavelets and adaptive approximation schemes. J. Chem. Phys. 117 (2002) 3625–3638. CrossRef
P.-A. Nitsche, Best N-term approximation spaces for sparse grids, Research Report No. 2003-11, Seminar für Angewandte Mathematik, ETH Zürich.
R. Schneider, Multiskalen- und Wavelet-Matrixkompression, Teubner, Stuttgart (1998).
Yanai, T., Fann, G.I., Gan, Z., Harrison, R.J. and Beylkin, G., Multiresolution quantum chemistry in multiwavelet basis: Hartree-Fock exchange. J. Chem. Phys. 121 (2004) 6680–6688. CrossRef
Yanai, T., Fann, G.I., Gan, Z., Harrison, R.J. and Beylkin, G., Multiresolution quantum chemistry in multiwavelet basis: Analytic derivatives for Hartree-Fock and density functional theory. J. Chem. Phys. 121 (2004) 2866–2876. CrossRef
Yserentant, H., On the regularity of the electronic Schrödinger equation in Hilbert spaces of mixed derivatives. Numer. Math. 98 (2004) 731–759. CrossRef
Yserentant, H., Sparse grid spaces for the numerical solution of the electronic Schrödinger equation. Numer. Math. 101 (2005) 381–389. CrossRef