Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T09:56:28.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Best N-term approximation in electronic structure calculations. II. Jastrow factors

Published online by Cambridge University Press:  16 June 2007

Heinz-Jürgen Flad ,
Wolfgang Hackbusch  and
Reinhold Schneider
Heinz-Jürgen Flad
Affiliation:
Max-Planck-Institut für Mathematik in den Naturwissenschaften, Inselstr. 22-26, 04103 Leipzig, Germany. [email protected]
Wolfgang Hackbusch
Affiliation:
Max-Planck-Institut für Mathematik in den Naturwissenschaften, Inselstr. 22-26, 04103 Leipzig, Germany. [email protected]
Reinhold Schneider
Affiliation:
Institut für Informatik Christian-Albrechts-Universität zu Kiel, Christian-Albrechts-Platz 4, 24098 Kiel, Germany.
Get access

Abstract

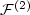We present a novel application of best N-term approximation theoryin the framework of electronic structure calculations. The paper focusses on thedescription of electron correlations within a Jastrow-type ansatz for thewavefunction. As a starting point we discuss certain natural assumptions onthe asymptotic behaviour of two-particle correlation functions $\mathcal{F}^{(2)}$ near electron-electron and electron-nuclear cusps. Basedon Nitsche's characterization of best N-term approximation spaces $A_{q}^{\alpha}(H^{1})$ 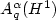, we prove that $\left.\mathcal{F}^{(2)}\inA_{q}^{\alpha}(H^{1})\right.$ 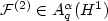for q>1 and $\alpha=\frac{1}{q}-\frac{1}{2}$ 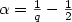with respect to a certain class of anisotropic wavelet tensor product bases.Computational arguments are given in favour of this specific class compared toother possible tensor product bases. Finally, we compare the approximationproperties of wavelet bases with standard Gaussian-type basis sets frequentlyused in quantum chemistry.


Keywords

Best N-term approximationwaveletselectroncorrelationsJastrow factor.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 41 , Issue 2: Special issue on Molecular Modelling , March 2007 , pp. 261 - 279
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

S. Agmon, Lectures on exponential decay of solutions of second-order elliptic equations: Bounds on eigenfunctions of N-body Schrödinger operators, Mathematical Notes 29. Princeton University Press (1982).
Bungartz, H.-J. and Griebel, M., Sparse grids. Acta Numer. 13 (2004) 147–269. CrossRef
Campbell, C.E., Krotscheck, E. and Pang, T., Electron correlations in atomic systems. Phys. Rep. 223 (1992) 1–42. CrossRef
Ceperley, D., Ground state of the fermion one-component plasma: A Monte Carlo study in two and three dimensions. Phys. Rev. B 18 (1978) 3126–3138. CrossRef
J.W. Clark, Variational theory of nuclear matter, in Progress in Nuclear and Particle Physics, Vol. 2, D.H. Wilkinson Ed., Pergamon, Oxford (1979) 89–199.
E.T. Copson, Asymptotic Expansions. Cambridge University Press, Cambridge (1967).
Dahmen, W., Prößdorf, S. and Schneider, R., Wavelet approximation methods for pseudodifferential equations. II: Matrix compression and fast solution. Adv. Comp. Maths. 1 (1993) 259–335. CrossRef
Dahmen, W., Prößdorf, S. and Schneider, R., Wavelet approximation methods for pseudodifferential equations. I: Stability and convergence. Math. Z. 215 (1994) 583–620. CrossRef
DeVore, R.A., Nonlinear approximation. Acta Numer. 7 (1998) 51–150. CrossRef
DeVore, R.A., Jawerth, B. and Popov, V., Compression of wavelet decompositions. Amer. J. Math. 114 (1992) 737–785. CrossRef
DeVore, R.A., Konyagin, S.V. and Temlyakov, V.N., Hyperbolic wavelet approximation. Constr. Approx. 14 (1998) 1–26. CrossRef
Drummond, N.D., Towler, M.D. and Needs, R.J., Jastrow correlation factor for atoms, molecules, and solids. Phys. Rev. B 70 (2004) 235119. CrossRef
Flad, H.-J. and Savin, A., Transfer of electron correlation from the electron gas to inhomogeneous systems via Jastrow factors. Phys. Rev. A. 50 (1994) 3742–3746. CrossRef
Flad, H.-J. and Savin, A., A new Jastrow factor for atoms and molecules, using two-electron systems as a guiding principle. J. Chem. Phys. 103 (1995) 691–697. CrossRef
Flad, H.-J., Hackbusch, W., Kolb, D. and Schneider, R., Wavelet approximation of correlated wavefunctions. I. Basics. J. Chem. Phys. 116 (2002) 9641–9657. CrossRef
Flad, H.-J., Hackbusch, W., Luo, H. and Kolb, D., Diagrammatic multiresolution analysis for electron correlations. Phys. Rev. B 71 (2005) 125115. CrossRef
Flad, H.-J., Hackbusch, W. and Schneider, R., Best N-term approximation in electronic structure calculations. I. One-electron reduced density matrix. ESAIM: M2AN 40 (2006) 49–61. CrossRef
Fournais, S., Hoffmann-Ostenhof, M., Hoffmann-Ostenhof, T. and Ostergaard, T. S orensen, Sharp regularity results for Coulombic many-electron wave functions. Commun. Math. Phys. 255 (2005) 183–227. CrossRef
Freund, D.E., Huxtable, B.D. and Morgan III, J.D., Variational calculations on the helium isoelectronic sequence. Phys. Rev. A 29 (1984) 980–982. CrossRef
P. Fulde, Electron Correlations in Molecules and Solids, 2nd edition. Springer, Berlin (1993).
Fulde, P., Ground-state wave functions and energies of solids. Int. J. Quant. Chem. 76 (2000) 385–395. 3.0.CO;2-H>CrossRef
Garcke, J. and Griebel, M., On the computation of the eigenproblems of hydrogen and helium in strong magnetic and electric fields with the sparse grid combination technique. J. Comp. Phys. 165 (2000) 694–716. CrossRef
Gaudoin, R., Nekovee, M., Foulkes, W.M.C., Needs, R.J. and Rajagopal, G., Inhomogeneous random-phase approximation and many-electron trial wave functions. Phys. Rev. B 63 (2001) 115115. CrossRef
Hackbusch, W., Khoromskij, B.N. and Tyrtyshnikov, E., Hierarchical Kronecker tensor-product approximation. J. Numer. Math. 13 (2005) 119–156. CrossRef
Halkier, A., Helgaker, T., Jørgensen, P., Klopper, W., Koch, H., Olsen, J. and Wilson, A.K., Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 286 (1998) 243–252. CrossRef
Helgaker, T., Klopper, W., Koch, H. and Noga, J., Basis-set convergence of correlated calculations on water. J. Chem. Phys. 106 (1997) 9639–9646. CrossRef
T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory. Wiley, New York (1999).
Hill, R.N., Rates of convergence and error estimation formulas for the Rayleigh-Ritz variational method. J. Chem. Phys. 83 (1985) 1173–1196. CrossRef
Hoffmann-Ostenhof, M. and Seiler, R., Cusp conditions for eigenfunctions of n-electron systems. Phys. Rev. A 23 (1981) 21–23. CrossRef
Hoffmann-Ostenhof, M., Hoffmann-Ostenhof, T. and Stremnitzer, H., Local properties of Coulombic wave functions. Commun. Math. Phys. 163 (1994) 185–215. CrossRef
Huang, C.-J., Umrigar, C.J. and Nightingale, M.P., Accuracy of electronic wave functions in quantum Monte Carlo: The effect of high-order correlations. J. Chem. Phys. 107 (1997) 3007–3013. CrossRef
Kato, T., On the eigenfunctions of many-particle systems in quantum mechanics. Commun. Pure Appl. Math. 10 (1957) 151–177. CrossRef
Krotscheck, E., Variations on the electron gas. Ann. Phys. (N.Y.) 155 (1984) 1–55. CrossRef
Krotscheck, E., Theory of inhomogeneous quantum systems. III. Variational wave functions for Fermi fluids. Phys. Rev. B 31 (1985) 4267–4278. CrossRef
Krotscheck, E., Kohn, W. and Qian, G.-X., Theory of inhomogeneous quantum systems. IV. Variational calculations of metal surfaces. Phys. Rev. B 32 (1985) 5693–5712. CrossRef
Kutzelnigg, W., r 12-Dependent terms in the wave function as closed sums of partial wave amplitudes for large l. Theoret. Chim. Acta 68 (1985) 445–469. CrossRef
Kutzelnigg, W. and Morgan III, J.D., Rates of convergence of the partial-wave expansions of atomic correlation energies. J. Chem. Phys. 96 (1992) 4484–4508. CrossRef
Luo, H., Kolb, D., Flad, H.-J., Hackbusch, W. and Koprucki, T., Wavelet approximation of correlated wavefunctions. II. Hyperbolic wavelets and adaptive approximation schemes. J. Chem. Phys. 117 (2002) 3625–3638. CrossRef
Luo, H., Kolb, D., Flad, H.-J. and Hackbusch, W., Perturbative calculation of Jastrow factors. Phys. Rev. B. 75 (2007) 125111. CrossRef
Nitsche, P.-A., Sparse approximation of singularity functions. Constr. Approx. 21 (2005) 63–81.
Nitsche, P.-A., Best N-term approximation spaces for tensor product wavelet bases. Constr. Approx. 24 (2006) 49–70. CrossRef
Pang, T., Campbell, C.E. and Krotscheck, E., Local structure of electron correlations in atomic systems. Chem. Phys. Lett. 163 (1989) 537–541. CrossRef
Schmidt, K.E. and Moskowitz, J.W., Correlated Monte Carlo wave functions for the atoms He through Ne. J. Chem. Phys. 93 (1990) 4172–4178. CrossRef
E.M. Stein, Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton University Press (1993).
Stollhoff, G., The local ansatz extended. J. Chem. Phys. 105 (1996) 227–234. CrossRef
Stollhoff, G. and Fulde, P., On the computation of electronic correlation energies within the local approach. J. Chem. Phys. 73 (1980) 4548–4561. CrossRef
Talman, J.D., Linked-cluster expansion for Jastrow-type wave functions and its application to the electron-gas problem. Phys. Rev. A 10 (1974) 1333–1344. CrossRef
Talman, J.D., Variational calculation for the electron gas at intermediate densities. Phys. Rev. A 13 (1976) 1200–1208. CrossRef
Umrigar, C.J., Wilson, K.G. and Wilkins, J.W., Optimized trial wave functions for quantum Monte Carlo calculations. Phys. Rev. Lett. 60 (1988) 1719–1722. CrossRef
Williamson, A.J., Kenny, S.D., Rajagopal, G., James, A.J., Needs, R.J., Fraser, L.M., Foulkes, W.M.C. and Maccallum, P., Optimized wavefunctions for quantum Monte Carlo studies of atoms and solids. Phys. Rev. B 53 (1996) 9640–9648. CrossRef
Yserentant, H., On the regularity of the electronic Schrödinger equation in Hilbert spaces of mixed derivatives. Numer. Math. 98 (2004) 731–759. CrossRef
Yserentant, H., Sparse grid spaces for the numerical solution of the electronic Schrödinger equation. Numer. Math. 101 (2005) 381–389. CrossRef