Sparse finite element approximation of high-dimensional transport-dominated diffusion problems

Abstract

We develop the analysis of stabilized sparse tensor-productfinite element methods for high-dimensional,non-self-adjoint and possibly degenerate second-order partialdifferential equations of the form $-a:\nabla\nabla u + b \cdot \nabla u + cu = f(x)$ 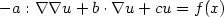, $x \in\Omega = (0,1)^d \subset \mathbb{R}^d$ 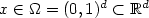,where $a \in \mathbb{R}^{d\times d}$ 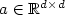is a symmetric positive semidefinite matrix,using piecewise polynomials ofdegree p ≥ 1. Our convergence analysis is based on newhigh-dimensional approximation results in sparse tensor-productspaces. We show that the error between the analytical solution u and its stabilizedsparse finite element approximation u _h on a partition ofΩ of mesh size h = h_L = 2^-L satisfies thefollowing bound in the streamline-diffusion norm $|||\cdot|||_{\rm SD}$ 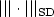,provided u belongs to the space $\mathcal{H}^{k+1}(\Omega)$ 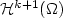of functionswith square-integrable mixed (k+1)st derivatives: \[|||u-u_h|||_{\rm SD}\leq C_{p,t} d^2 \max\{(2-p)_+,\kappa_0^{d-1},\kappa_1^d\} (|\sqrt{a}| h_L^t+ |b|^{\frac{1}{2}} h_L^{t+\frac{1}{2}} + c^{\frac{1}{2}} h_L^{t+1} \!)|u|_{\mathcal{H}^{t+1}(\Omega)}, \qquad \qquad \qquad\] 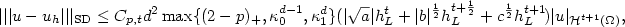where $\kappa_i=\kappa_i(p,t,L)$ 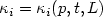, i=0,1, and $1 \leq t \leq \min(k,p)$ 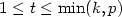.We show, under various mild conditionsrelating L to p, L to d, or p to d,that in the case of elliptic transport-dominateddiffusion problems $\kappa_0, \kappa_1 \in (0,1)$ 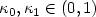, and hence for p ≥ 1 the'error constant' $C_{p,t} d^2 \max\{(2-p)_+,\kappa_0^{d-1},\kappa_1^d\}$ 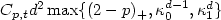exhibits exponential decay as d → ∞; in the case of ageneral symmetric positive semidefinite matrix a,the error constant is shown to grow no faster than $\mathcal{O}(d^2)$ 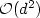.In any case, in the absence of assumptions that relate L, p and d,the error $|||u - u_h|||_{\rm SD}$ 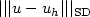is still bounded by $\kappa_\ast^{d-1}|\log_2 h_L|^{d-1}\mathcal{O}(|\sqrt{a}| h_L^t+ |b|^{\frac{1}{2}} h_L^{t+\frac{1}{2}}+c^{\frac{1}{2}} h_L^{t+1})$ 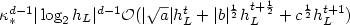, where $\kappa_\ast \in (0,1)$ 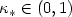for all L, p, d ≥ 2.