Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T01:29:04.006Z Has data issue: false hasContentIssue false
  • English
  • Français

A new H(div)-conforming p-interpolation operator in two dimensions

Published online by Cambridge University Press:  02 August 2010

Alexei Bespalov  and
Norbert Heuer
Alexei Bespalov
Affiliation:
Department of Mathematical Sciences, Brunel University, Uxbridge, West London UB8 3PH, UK. [email protected]
Norbert Heuer
Affiliation:
ANESTOC and Facultad de Matemáticas, Pontificia Universidad Católica de Chile, Avenida Vicuña Mackenna 4860, Santiago, Chile. [email protected]
Get access

Abstract

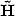In this paper we construct a new H(div)-conforming projection-based p-interpolation operator that assumes only Hr(K) $\cap$${\bf \tilde H}$-1/2(div, K)-regularity (r > 0) on the reference element (either triangle or square) K. We show that this operator is stable with respect to polynomial degrees and satisfies the commuting diagram property. We also establish an estimate for the interpolation error in the norm of the space ${\bf \tilde H}$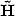-1/2(div, K), which is closely related to the energy spaces for boundary integral formulations of time-harmonic problems of electromagnetics in three dimensions.

Keywords

p-interpolationerror estimationMaxwell's equationsboundary element method.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 45 , Issue 2 , March 2011 , pp. 255 - 275
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babuška, I. and Suri, M., The h – p version of the finite element method with quasiuniform meshes. RAIRO Modél. Math. Anal. Numér. 21 (1987) 199–238. CrossRef
Babuška, I., Craig, A., Mandel, J. and Pitkäranta, J., Efficient preconditioning for the p-version finite element method in two dimensions. SIAM J. Numer. Anal. 28 (1991) 624–661. CrossRef
Bespalov, A. and Heuer, N., Optimal error estimation for H(curl)-conforming p-interpolation in two dimensions. SIAM J. Numer. Anal. 47 (2009) 3977–3989. CrossRef
A. Bespalov and N. Heuer, Natural p-BEM for the electric field integral equation on screens. IMA J. Numer. Anal. (2010) DOI:10.1093/imanum/drn072. CrossRef
Bespalov, A. and Heuer, N., Thehp – BEMS with quasi-uniform meshes for the electric field integral equation on polyhedral surfaces: a priori error analysis. Appl. Numer. Math. 60 (2010) 705–718. CrossRef
A. Bespalov, N. Heuer and R. Hiptmair, Convergence of the natural hp-BEM for the electric field integral equation on polyhedral surfaces. arXiv:0907.5231 (2009).
Boffi, D., Demkowicz, L. and Costabel, M., Discrete compactness for the p and hp 2D edge finite elements. Math. Models Methods Appl. Sci. 13 (2003) 1673–1687. CrossRef
Boffi, D., Costabel, M., Dauge, M. and Demkowicz, L., Discrete compactness for the hp version of rectangular edge finite elements. SIAM J. Numer. Anal. 44 (2006) 979–1004. CrossRef
D. Boffi, M. Costabel, M. Dauge, L. Demkowicz and R. Hiptmair, Discrete compactness for the p -version of discrete differential forms. arXiv:0909.5079 (2009).
F. Brezzi and M. Fortin, Mixed and Hybrid Finite Element Methods, Springer Series in Computational Mathematics 15. Springer-Verlag, New York (1991).
Buffa, A., Remarks on the discretization of some noncoercive operator with applications to heterogeneous Maxwell equations. SIAM J. Numer. Anal. 43 (2005) 1–18. CrossRef
Buffa, A. and Christiansen, S.H., The electric field integral equation on Lipschitz screens: definitions and numerical approximation. Numer. Math. 94 (2003) 229–267. CrossRef
Buffa, A. and Ciarlet, P., On, Jr. traces for functional spaces related to Maxwell's equations, Part II: Hodge decompositions on the boundary of Lipschitz polyhedra and applications. Math. Methods Appl. Sci. 24 (2001) 31–48. 3.0.CO;2-X>CrossRef
Buffa, A., Hiptmair, R., von Petersdorff, T. and Schwab, C., Boundary element methods for Maxwell transmission problems in Lipschitz domains. Numer. Math. 95 (2003) 459–485. CrossRef
Costabel, M. and Dauge, M., Singularities of electromagnetic fields in polyhedral domains. Arch. Rational Mech. Anal. 151 (2000) 221–276. CrossRef
Costabel, M. and McIntosh, A., Bogovskiĭ, On and regularized Poincaré integral operators for de Rham complexes on Lipschitz domains. Math. Z. 265 (2010) 297–320. CrossRef
Costabel, M., Dauge, M. and Demkowicz, L., Polynomial extension operators for H 1, H(curl) and H(div)-spaces on a cube. Math. Comp. 77 (2008) 1967–1999. CrossRef
L. Demkowicz, Polynomial exact sequences and projection-based interpolation with applications to Maxwell equations, in Mixed Finite Elements, Compatibility Conditions and Applications, D. Boffi, F. Brezzi, L. Demkowicz, R. Duran, R. Falk and M. Fortin Eds., Lect. Notes in Mathematics 1939, Springer-Verlag, Berlin (2008) 101–158.
Demkowicz, L. and Babuška, I., p interpolation error estimates for edge finite elements of variable order in two dimensions. SIAM J. Numer. Anal. 41 (2003) 1195–1208. CrossRef
Dorr, M.R., The approximation theory for the p-version of the finite element method. SIAM J. Numer. Anal. 21 (1984) 1180–1207. CrossRef
Heuer, N., Additive Schwarz method for the p-version of the boundary element method for the single layer potential operator on a plane screen. Numer. Math. 88 (2001) 485–511. CrossRef
R. Hiptmair, Discrete compactness for the p-version of tetrahedral edge elements. Seminar for Applied Mathematics, ETH Zürich, Switzerland (2008) arXiv:0901.0761.
J.-L. Lions and E. Magenes, Non-Homogeneous Boundary Value Problems and Applications I. Springer-Verlag, New York (1972).
S.E. Mikhailov, About traces, extensions and co-normal derivative operators on Lipschitz domains, in Integral Methods in Science and Engineering: Techniques and Applications, C. Constanda and S. Potapenko Eds., Birkhäuser, Boston (2008) 149–160.
R.E. Roberts and J.-M. Thomas, Mixed and hybrid methods, in Handbook of Numerical Analysis II, P.G. Ciarlet and J.-L. Lions Eds., Amsterdam, North-Holland (1991) 523–639.