Article contents
Impact of the variations of the mixing length in a first order turbulentclosure system
Published online by Cambridge University Press: 15 May 2002
Abstract
This paper is devoted to the study of a turbulentcirculation model. Equations are derived from the “Navier-Stokes turbulentkinetic energy” system. Some simplifications are performed but attentionis focused on non linearities linked to turbulent eddy viscosity $\nu _{t}$ 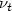 . The mixing length $\ell $
. The mixing length $\ell $ 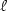 acts as a parameter which controls theturbulent part in $\nu _{t}$
acts as a parameter which controls theturbulent part in $\nu _{t}$ 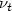 . The main theoretical results that we haveobtained concern the uniqueness of the solution for bounded eddy viscositiesand small values of $\ell $
. The main theoretical results that we haveobtained concern the uniqueness of the solution for bounded eddy viscositiesand small values of $\ell $ 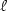 and its asymptotic decreasing as $\ell\rightarrow \infty $
and its asymptotic decreasing as $\ell\rightarrow \infty $ 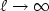 in more general cases. Numerical experimentsillustrate but also allow to extend these theoretical results: uniqueness isproved only for $\ell $
in more general cases. Numerical experimentsillustrate but also allow to extend these theoretical results: uniqueness isproved only for $\ell $ 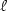 small enough while regular solutions are numericallyobtained for any values of $\ell $
small enough while regular solutions are numericallyobtained for any values of $\ell $ 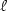 . A convergence theorem is proved forturbulent kinetic energy: $k_{\ell }\rightarrow 0$
. A convergence theorem is proved forturbulent kinetic energy: $k_{\ell }\rightarrow 0$ 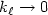 as $\ell \rightarrow\infty ,$
as $\ell \rightarrow\infty ,$ 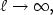 but for velocity $u_{\ell }$
but for velocity $u_{\ell }$ 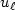 we obtain only weaker results.Numerical results allow to conjecture that $k_{\ell }\rightarrow 0,$
we obtain only weaker results.Numerical results allow to conjecture that $k_{\ell }\rightarrow 0,$ 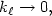 $\nu_{t}\rightarrow \infty $
$\nu_{t}\rightarrow \infty $ 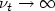 and $u_{\ell }\rightarrow 0$
and $u_{\ell }\rightarrow 0$  as $\ell \rightarrow\infty .$
as $\ell \rightarrow\infty .$ 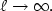 So we can conjecture that this classical turbulent model obtainedwith one degree of closure regularizes the solution.
So we can conjecture that this classical turbulent model obtainedwith one degree of closure regularizes the solution.
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 36 , Issue 2 , March 2002 , pp. 345 - 372
- Copyright
- © EDP Sciences, SMAI, 2002
References
- 12
- Cited by


