Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-16T11:18:56.475Z Has data issue: false hasContentIssue false
  • English
  • Français

The G method for heterogeneous anisotropic diffusionon general meshes

Published online by Cambridge University Press:  17 March 2010

Léo Agélas ,
Daniele A. Di Pietro  and
Jérôme Droniou
Léo Agélas
Affiliation:
IFP, 1 & 4 av. du Bois-Préau, 92852 Rueil-Malmaison Cedex, France. [email protected]; [email protected]
Daniele A. Di Pietro
Affiliation:
IFP, 1 & 4 av. du Bois-Préau, 92852 Rueil-Malmaison Cedex, France. [email protected]; [email protected]
Jérôme Droniou
Affiliation:
Université Montpellier 2, Institut de Mathématiques et Modélisation de Montpellier, CC 051, Place Eugène Bataillon, 34095 Montpellier Cedex 05, France. [email protected]
Get access

Abstract

In the present work we introduce a new family of cell-centered Finite Volume schemes for anisotropic and heterogeneous diffusion operators inspired by the MPFA L method.A very general framework for the convergence study of finite volume methods is provided and then used to establish the convergence of the new method.Fairly general meshes are covered and a computable sufficient criterion for coercivity is provided. 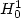In order to guarantee consistency in the presence of heterogeneous diffusivity, we introduce a non-standard test space in $H_0^1$ (Ω) and prove its density. Thorough assessment on a set of anisotropic heterogeneous problems as well as a comparison with classical multi-point Finite Volume methods is provided.

Keywords

Finite volume methodsheterogeneous anisotropic diffusionMPFAconvergence analysis
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 44 , Issue 4 , July 2010 , pp. 597 - 625
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aavatsmark, I., An introduction to multipoint flux approximations for quadrilateral grids. Comput. Geosci. 6 (2002) 405–432. CrossRef
I. Aavatsmark, T. Barkve, Ø. Bøe and T. Mannseth, Discretization on non-orthogonal, curvilinear grids for multi-phase flow, in Proc. of the 4th European Conf. on the Mathematics of Oil Recovery (Røros, Norway), Vol. D (1994).
I. Aavatsmark, G.T. Eigestad, B.T. Mallison, J.M. Nordbotten and E. Øian, A new finite volume approach to efficient discretization on challeging grids, in Proc. SPE 106435, Houston, USA (2005).
Aavatsmark, I., Eigestad, G.T., Klausen, R.A., Wheeler, M.F. and Yotov, I., Convergence of a symmetric MPFA method on quadrilateral grids. Comput. Geosci. 11 (2007) 333–345. CrossRef
Aavatsmark, I., Eigestad, G.T., Mallison, B.T. and Nordbotten, J.M., A compact multipoint flux approximation method with improved robustness. Numer. Methods Partial Differ. Equ. 24 (2008) 1329–1360. CrossRef
L. Agélas and D.A. Di Pietro, A symmetric finite volume scheme for anisotropic heterogeneous second-order elliptic problems, in Finite Volumes for Complex Applications, V.R. Eymard and J.-M. Hérard Eds., John Wiley & Sons (2008) 705–716.
L. Agélas and R. Masson, Convergence of the finite volume MPFA O scheme for heterogeneous anisotropic diffusion problems on general meshes. C. R. Acad. Sci. Paris, Sér. I 346 (2008) 1007–1012.
L. Agélas and R. Masson, Convergence of finite volume MPFA O type schemes for heterogeneous anisotropic diffusion problems on general meshes. Preprint available at http://hal.archives-ouvertes.fr/hal-00340159/fr (2008).
L. Agélas, D.A. Di Pietro and R. Masson, A symmetric and coercive finite volume scheme for multiphase porous media flow with applications in the oil industry, in Finite Volumes for Complex Applications, V.R. Eymard and J.-M. Hérard Eds., John Wiley & Sons (2008) 35–52.
Agélas, L., Di Pietro, D.A., Eymard, R. and Masson, R., An abstract analysis framework for nonconforming approximations of diffusion problems on general meshes. IJFV 7 (2010) 1–29.
S. Balay, W.D. Gropp, L.C. McInnes and B.F. Smith, Efficient management of parallelism in object oriented numerical software libraries, in Modern Software Tools in Scientific Computing, E. Arge, A.M. Bruaset and H.P. Langtangen Eds., Birkhäuser Press (1997) 163–202.
S. Balay, K. Buschelman, W.D. Gropp, D. Kaushik, M.G. Knepley, L.C. McInnes, B.F. Smith and H. Zhang, PETSc Web page (2001) www.mcs.anl.gov/petsc.
S. Balay, K. Buschelman, V. Eijkhout, W.D. Gropp, D. Kaushik, M.G. Knepley, L.C. McInnes, B.F. Smith and H. Zhang, PETSc users manual. Tech. Report ANL-95/11 – Revision 2.1.5, Argonne National Laboratory (2004).
Brezzi, F., Lipnikov, K. and Shashkov, M., Convergence of mimetic finite difference methods for diffusion problems on polyhedral meshes. SIAM J. Numer. Anal. 45 (2005) 1872–1896. CrossRef
Brezzi, F., Lipnikov, K. and Simoncini, V., A family of mimetic finite difference methods on polygonal and polyhedral meshes. Math. Mod. Meths. Appli. Sci. 15 (2005) 1533–1553. CrossRef
Brezzi, F., Lipnikov, K. and Shashkov, M., Convergence of mimetic finite difference methods for diffusion problems on polyhedral meshes with curved faces. Math. Mod. Meths. Appli. Sci. 26 (2006) 275–298. CrossRef
D.A. Di Pietro and A. Ern, Discrete functional analysis tools for discontinuous Galerkin methods with application to the incompressible Navier-Stokes equations. Math. Comp. (2010), preprint available at http://hal.archives-ouvertes.fr/hal-00278925/fr/.
Droniou, J., A density result in Sobolev spaces. J. Math. Pures Appl. 81 (2002) 697–714. CrossRef
Droniou, J. and Eymard, R., A mixed finite volume scheme for anisotropic diffusion problems on any grid. Numer. Math. 105 (2006) 35–71. CrossRef
Droniou, J., Eymard, R., Gallouët, T. and Herbin, R., A unified approach to Mimetic Finite Difference, Hybrid Finite Volume and Mixed Finite Volume methods. Maths. Models Methods Appl. Sci. 20 (2010) 1–31.
M.G. Edwards and C.F. Rogers, A flux continuous scheme for the full tensor pressure equation, in Proc. of the 4th European Conf. on the Mathematics of Oil Recovery (Røros, Norway), Vol. D (1994).
R. Eymard, T. Gallouët and R. Herbin, The finite volume method, Ph.G. Charlet and J.-L. Lions Eds., North Holland (2000).
Eymard, R., Herbin, R. and Latché, J.C., Convergence analysis of a colocated finite volume scheme for the incompressible Navier-Stokes equations on general 2D or 3D meshes. SIAM J. Numer. Anal. 45 (2007) 1–36. CrossRef
R. Eymard, T. Gallouët and R. Herbin, Discretization of heterogeneous and anisotropic diffusion problems on general non-conforming meshes. SUSHI: a scheme using stabilization and hybrid interfaces. IMA J. Numer. Anal. (2009) doi: 10.1093/imanum/drn084. CrossRef
Vohralík, M., Equivalence between lowest-order mixed finite element and multi-point finite volume methods on simplicial meshes. ESAIM: M2AN 40 (2006) 367–391. CrossRef