Article contents
Computation of bifurcated branches in a free boundary problem arising in combustion theory
Published online by Cambridge University Press: 15 April 2002
Abstract
We consider a parabolic 2D Free Boundary Problem, with jump conditions at the interface. Its planar travelling-wave solutions are orbitally stableprovided the bifurcation parameter $u_*$ 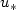 does not exceed a critical value $u_{*}^{c}$
does not exceed a critical value $u_{*}^{c}$ 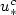 . The latter isthe limit of a decreasing sequence $(u_{*}^{k})$
. The latter isthe limit of a decreasing sequence $(u_{*}^{k})$ 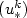 of bifurcation points. The paper deals with the study of the 2D bifurcated branchesfrom the planar branch, for small k. Our technique is based on the elimination of the unknown front, turning the problem into a fully nonlinear one, to which we canapply the Crandall-Rabinowitz bifurcation theorem for a local study.We point out that the fully nonlinear reformulation of the FBP can also serve to developefficient numerical schemes in view of global information, such as techniques based on arc length continuation.
of bifurcation points. The paper deals with the study of the 2D bifurcated branchesfrom the planar branch, for small k. Our technique is based on the elimination of the unknown front, turning the problem into a fully nonlinear one, to which we canapply the Crandall-Rabinowitz bifurcation theorem for a local study.We point out that the fully nonlinear reformulation of the FBP can also serve to developefficient numerical schemes in view of global information, such as techniques based on arc length continuation.
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 34 , Issue 2: Special issue for R. Teman's 60th birthday , March 2000 , pp. 223 - 339
- Copyright
- © EDP Sciences, SMAI, 2000
References
- 3
- Cited by


