Adaptive modeling for free-surface flows

Abstract

This work represents a first step towards the simulation of the motion of water in a complex hydrodynamic configuration, such asa channel network or a river delta, by means of a suitable“combination” of different mathematicalmodels. In this framework a wide spectrum of space and time scales is involveddue to the presence of physical phenomena ofdifferent nature. Ideally, moving from a hierarchy of hydrodynamic models, one should solvethroughout the whole domain the most complex model (with solution $u_{\rm{fine}}$ 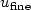) to accuratelydescribe all the physical features of the problem at hand. In our approach instead,for a user-defined output functional ${\cal F}$ 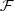, we aim to approximate,within a prescribed tolerance τ, the value ${\cal F}(u_{\rm{fine}})$ 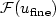by means of the quantity ${\cal F}(u_{\rm{adapted}})$ 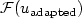, $u_{\rm{adapted}}$ 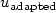being the so-called adapted solution solving thesimpler models on most of the computational domain while confining the complex ones only on a restricted region. Moving fromthe simplified setting where only two hydrodynamic models, fine and coarse, are considered, weprovide an efficient tool able to automatically selectthe regions of the domain where the coarsemodel rather than the fine one are to be solved, while guaranteeing $|{\cal F}(u_{\rm{fine}})-{\cal F}(u_{\rm{adapted}})|$ 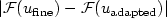below the tolerance τ.This goal is achieved via a suitable a posteriori modeling error analysisdeveloped in the framework of a goal-oriented theory.We extend the dual-based approach provided in [Braack and Ern,Multiscale Model Sim.1 (2003) 221–238],for steady equations to the case of a generic time-dependent problem.Then this analysis is specialized to the case we areinterested in, i.e. the free-surface flows simulation, by emphasizing the crucial issue of the time discretization for both the primal and the dualproblems. Finally, inthe last part of the paper a widespread numerical validation is carried out.