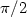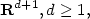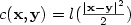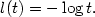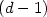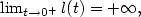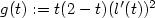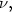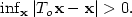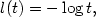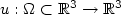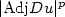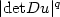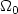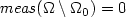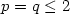In this paper, weconsider probability measures μ and ν on a d-dimensionalsphere in ${\bf R}^{d+1}, d \geq 1,$ 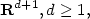 and cost functions of the form $c({\bf x},{\bf y})=l(\frac{|{\bf x}-{\bf y}|^2}{2})$
and cost functions of the form $c({\bf x},{\bf y})=l(\frac{|{\bf x}-{\bf y}|^2}{2})$ 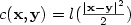 that generalize those arising in geometric optics where $l(t)=-\log t.$
that generalize those arising in geometric optics where $l(t)=-\log t.$ 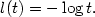 We prove that if μ and ν vanish on $(d-1)$
We prove that if μ and ν vanish on $(d-1)$ 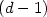 -rectifiable sets,if |l'(t)|>0, $\lim_{t\rightarrow 0^+}l(t)=+\infty,$
-rectifiable sets,if |l'(t)|>0, $\lim_{t\rightarrow 0^+}l(t)=+\infty,$ 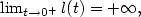 and $g(t):=t(2-t)(l'(t))^2$
and $g(t):=t(2-t)(l'(t))^2$ 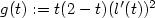 is monotone then thereexists a unique optimal map T o that transports μ onto $\nu,$
is monotone then thereexists a unique optimal map T o that transports μ onto $\nu,$ 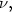 whereoptimality is measured against c. Furthermore, $\inf_{{\bf x}}|T_o{\bf x}-{\bf x}|>0.$
whereoptimality is measured against c. Furthermore, $\inf_{{\bf x}}|T_o{\bf x}-{\bf x}|>0.$ 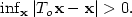 Our approach is based on direct variational arguments.In the special case when $l(t)=-\log t,$
Our approach is based on direct variational arguments.In the special case when $l(t)=-\log t,$ 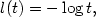 existence of optimal maps on thesphere was obtained earlier in [Glimm and Oliker, J. Math. Sci.117 (2003) 4096-4108]and [Wang, Calculus of Variations and PDE's20 (2004) 329-341] under more restrictive assumptions. In these studies, it was assumed that either μ and ν are absolutelycontinuous with respect to the d-dimensional Haussdorff measure, or they have disjoint supports. Another aspect of interestin this work is that it is in contrast with the work in[Gangbo and McCann, Quart. Appl. Math.58 (2000) 705-737] where it is proved that when l(t)=t thenexistence of an optimal map fails when μ and ν are supported by Jordan surfaces.
existence of optimal maps on thesphere was obtained earlier in [Glimm and Oliker, J. Math. Sci.117 (2003) 4096-4108]and [Wang, Calculus of Variations and PDE's20 (2004) 329-341] under more restrictive assumptions. In these studies, it was assumed that either μ and ν are absolutelycontinuous with respect to the d-dimensional Haussdorff measure, or they have disjoint supports. Another aspect of interestin this work is that it is in contrast with the work in[Gangbo and McCann, Quart. Appl. Math.58 (2000) 705-737] where it is proved that when l(t)=t thenexistence of an optimal map fails when μ and ν are supported by Jordan surfaces.