Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T10:27:21.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Upper bounds for a class of energies containinga non-local term

Published online by Cambridge University Press:  31 July 2009

Arkady Poliakovsky
Arkady Poliakovsky*
Affiliation:
Fachbereich Mathematik, Universität Duisburg-Essen, Lotharstrasse 65, 47057 Duisburg, Germany. [email protected]
Get access

Abstract

In this paper we construct upper bounds for families offunctionals of the form

$$E_\varepsilon(\phi):=\int_\Omega\Big(\varepsilon |\nabla\phi|^2+\frac{1}{\varepsilon }W(\phi)\Big){\rm d}x+\frac{1}{\varepsilon }\int_{{\mathbb{R}}^N}|\nabla \bar H_{F(\phi)}|^2{\rm d}x$$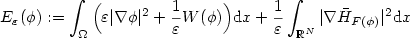

where Δ $\bar H_u$ 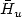= div { $\chi_\Omega$ 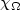u}. Particular cases of such functionals arise inMicromagnetics. We also use our technique to construct upper boundsfor functionals that appear in a variational formulation ofthe method of vanishing viscosity for conservation laws.

Keywords

Gamma-convergencemicromagneticsnon-local energy
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 4 , October 2010 , pp. 856 - 886
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alouges, F., Rivière, T. and Serfaty, S., Néel and cross-tie wall energies for planar micromagnetic configurations. ESAIM: COCV 8 (2002) 31–68. CrossRef
L. Ambrosio, N. Fusco and D. Pallara, Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs. Oxford University Press, New York (2000).
A. DeSimone, S. Müller, R.V. Kohn and F. Otto, Recent analytical developments in micromagnetics, in The Science of Hysteresis 2, G. Bertotti and I. Mayergoyz Eds., Elsevier Academic Press (2005) 269–381.
A. Hubert and R. Schäfer, Magnetic domains. Springer (1998).
Jin, W. and Kohn, R.V., Singular perturbation and the energy of folds. J. Nonlinear Sci. 10 (2000) 355–390. CrossRef
Poliakovsky, A., Upper bounds for singular perturbation problems involving gradient fields. J. Eur. Math. Soc. 9 (2007) 1–43.
Poliakovsky, A., Sharp upper bounds for a singular perturbation problem related to micromagnetics. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 6 (2007) 673–701.
Poliakovsky, A., A general technique to prove upper bounds for singular perturbation problems. J. Anal. Math. 104 (2008) 247–290. CrossRef
Poliakovsky, A., On a variational approach to the Method of Vanishing Viscosity for Conservation Laws. Adv. Math. Sci. Appl. 18 (2008) 429–451.
Rivière, T. and Serfaty, S., Limiting domain wall energy for a problem related to micromagnetics. Comm. Pure Appl. Math. 54 (2001) 294–338. 3.0.CO;2-S>CrossRef
Rivière, T. and Serfaty, S., Compactness, kinetic formulation and entropies for a problem related to mocromagnetics. Comm. Partial Differential Equations 28 (2003) 249–269. CrossRef