Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T10:34:16.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Unique Localization of Unknown Boundaries in a Conducting Medium from Boundary Measurements

Published online by Cambridge University Press:  15 September 2002

Bruno Canuto
Bruno Canuto*
Affiliation:
Laboratoire de Mathématiques Appliquées, UMR 7641, Université de Versailles, 45 avenue des États-Unis, 78035 Versailles Cedex, France; [email protected].
Get access

Abstract

We consider the problem of localizing an inaccessible piece I of the boundary of a conducting medium Ω, and a cavity D contained in Ω, from boundary measurements on the accessible part A of ∂Ω. Assuming that g(t,σ) is the given thermal flux for (t,σ) ∈ (0,T) x A, and that the corresponding output datum is the temperature u(T0,σ) measured at a given time T0 for σ ∈ Aout ⊂ A, we prove that I and D are uniquely localized from knowledge of all possible pairs of input-output data $(g,u(T_0)_{\mid A_{{\rm out}}})$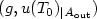. The same result holds when a mean value of the temperature is measured over a small interval of time.

Keywords

Inverse boundary value problemscavitiescorrosionuniqueness.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 7 , 2002 , pp. 1 - 22
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bryan, K. and Caudill, L.F., Inverse Problem, An in Thermal Imaging. SIAM J. Appl. Math. 56 (1996) 715-735. CrossRef
B. Canuto and O. Kavian, Determining Coefficients in a Class of Heat Equations via Boundary Measurements. SIAM J. Math. Anal. (to appear).
R. Courant and D. Hilbert, Methods of Mathematical Physics, Vol. 1. Wiley, New York (1953).
Garofalo, N. and Lin, F.H., Monotonicity Properties of Variational Integrals, A p Weights and Unique Continuation. Indiana Univ. Math. J. 35 (1986) 245-268. CrossRef
O.A. Ladyzhenskaja, V.A. Solonnikov and N.N. Uralceva, Linear and Quasilinear Equations of Parabolic Type. AMS, Providence, RI, Trans. Math. Monographs 23 (1968).
Rakesh, W.W. Symes, Uniqueness for an Inverse Problem for the Wave Equation. Comm. Partial Differential Equations 13 (1988) 87-96. CrossRef
Saut, J.-C. and Scheurer, B., Unique Continuation for Some Evolution Equations. J. Differential Equations 66 (1987) 118-139. CrossRef
Vessella, S., Stability Estimates in an Inverse Problem for a Three-Dimensional Heat Equation. SIAM J. Math. Anal. 28 (1997) 1354-1370. CrossRef
S. Vessella, Private Comunication.