Static Hedging of Barrier Options with a Smile: An Inverse Problem

Abstract

Let L be a parabolic second order differential operator on the domain $ \bar{\Pi}=\left[ 0,T\right] \times {\mathbb R}.$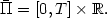 Given a function $\hat{u}: {\mathbb R\rightarrow R}$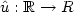 and $\hat{x}>0$ 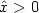such that the support of û is contained in $(-\infty ,-\hat{x}]$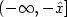, we let $\hat{y}:\bar{\Pi}\rightarrow {\mathbb R}$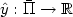 be the solution to the equation: \[ L\hat{y}=0,\text{\quad }\hat{y}|_{\{0\}\times {\mathbb R}}=\hat{u} . \]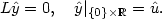 Given positive bounds $0<x_{0}<x_{1},$ 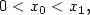we seek a function u with support in $\left[ x_{0},x_{1}\right] $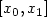 such that the corresponding solution y satisfies: \[ y(t,0)=\hat{y}(t,0)\quad \quad \forall t\in \left[ 0,T\right] . \]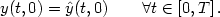 We prove in this article that, under some regularity conditions on the coefficients of L, continuous solutions are unique and dense in the sense that $\hat{y}|_{[0,T]\times \{0\}}$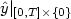 can be C⁰-approximated, but an exact solution does not exist in general. This result solves the problem of almost replicating a barrier option in the generalised Black–Scholes framework with a combination of European options, as stated by Carr et al. in [6].