Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T17:54:52.133Z Has data issue: false hasContentIssue false
  • English
  • Français

Some regularity results for minimal crystals

Published online by Cambridge University Press:  15 August 2002

L. Ambrosio ,
M. Novaga  and
E. Paolini
L. Ambrosio
Affiliation:
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy; [email protected].
M. Novaga
Affiliation:
Dipartimento di Matematica, Università di Pisa, via F. Buonarroti 2, 56126 Pisa, Italy.
E. Paolini
Affiliation:
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy; [email protected].
Get access

Abstract

We introduce an intrinsic notion of perimeter for subsets ofa general Minkowski space (i.e. a finite dimensional Banach space in which thenorm is not required to be even).We prove that this notion of perimeter is equivalent tothe usual definition of surface energy for crystals andwe study the regularity properties of the minimizers and the quasi-minimizers of perimeter.In the two-dimensional case we obtain optimal regularity results:apart from a singular set (which is ${\mathcal H}^1$ 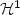-negligible and is empty whenthe unit ball is neither a triangle nor a quadrilateral), we find that quasi-minimizers can be locallyparameterized by means of a bi-lipschitz curve, while sets with prescribed bounded curvature are, locally, lipschitz graphs.

Keywords

Quasi-minimal setsWulff shapecrystalline norm.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 8: A tribute to JL Lions , 2002 , pp. 69 - 103
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almgren, F.J., Optimal isoperimetric inequalities. Indiana U. Math. J. 35 (1986) 451-547. CrossRef
Almgren, F.J. and Taylor, J., Flat flow is motion by crystalline curvature for curves with crystalline energies. J. Diff. Geom. 42 (1995) 1-22. CrossRef
Almgren, F.J., Taylor, J. and Wang, L., Curvature-driven flows: A variational approach. SIAM J. Control Optim. 31 (1993) 387-437. CrossRef
Amar, M. and Bellettini, G., A notion of total variation depending on a metric with discontinuous coefficients. Ann. Inst. H. Poincaré Anal. Non Linéaire 11 (1994) 91-133. CrossRef
L. Ambrosio, Corso introduttivo alla Teoria Geometrica della Misura ed alle Superfici Minime. Scuola Normale Superiore of Pisa (1997).
L. Ambrosio, N. Fusco and D. Pallara, Functions of bounded variation and free discontinuity problems. Oxford U. P. (2000).
Ambrosio, L., Caselles, V., Masnou, S. and Morel, J.M., Connected Components of Sets of Finite Perimeter and Applications to Image Processing. J. EMS 3 (2001) 213-266.
L. Ambrosio and E. Paolini, Partial regularity for the quasi minimizers of perimeter. Ricerche Mat. XLVIII (1999) 167-186.
Bellettini, G., Paolini, M. and Venturini, S., Some results on surface measures in Calculus of Variations. Ann. Mat. Pura Appl. 170 (1996) 329-359. CrossRef
Bombieri, E., Regularity theory for almost minimal currents. Arch. Rational Mech. Anal. 78 (1982) 99-130. CrossRef
H. Brezis, Opérateurs Maximaux Monotones. North Holland, Amsterdam (1973).
Y.D. Burago and V.A. Zalgaller, Geometric inequalities. Springer-Verlag, Berlin, Grundlehren der Mathematischen Wissenschaften XIV (1988).
G. David and S. Semmes, Uniform rectifiability and quasiminimizing sets of arbitrary codimension. Mem. Amer. Math. Soc. 687 (2000).
De Giorgi, E., Nuovi teoremi relativi alle misure (r-1)-dimensionali in uno spazio a r dimensioni. Ricerche Mat. 4 (1955) 95-113.
Federer, H., A note on the Gauss-Green theorem. Proc. Amer. Math. Soc. 9 (1958) 447-451. CrossRef
H. Federer, Geometric Measure Theory. Springer-Verlag, Berlin (1969).
Fleming, W.H., Functions with generalized gradient and generalized surfaces. Ann. Mat. 44 (1957) 93-103. CrossRef
Fonseca, I., The Wulff theorem revisited. Proc. Roy. Soc. London 432 (1991) 125-145. CrossRef
Fonseca, I. and Müller, S., A uniqueness proof for the Wulff theorem. Proc. Roy. Soc. Edinburgh 119 (1991) 125-136. CrossRef
E. Giusti, Minimal surfaces and functions of bounded variation. Birkhäuser, Boston-Basel-Stuttgart, Monogr. in Math. 80 (1984) XII.
Kirchheim, B., Rectifiable metric spaces: Local structure and regularity of the Hausdorff measure. Proc. AMS 121 (1994) 113-123. CrossRef
Luckhaus, S. and Modica, L., The Gibbs-Thompson relation within the gradient theory of phase transitions. Arch. Rational Mech. Anal. 107 (1989) 71-83. CrossRef
Morgan, F., The cone over the Clifford torus in ${\mathcal {\mathbb R}^4}$ is $\Phi$ -minimizing. Math. Ann. 289 (1991) 341-354. CrossRef
Morgan, F., French, C. and Greenleaf, S., Wulff clusters in R 2. J. Geom. Anal. 8 (1998) 97-115. CrossRef
Morse, A.P., Perfect blankets. Trans. Amer. Math. Soc. 61 (1947) 418-442. CrossRef
Taylor, J., Crystalline variational problems. Bull. Amer. Math. Soc. (N.S.) 84 (1978) 568-588. CrossRef
J. Taylor, Motion of curves by crystalline curvature, including triple junctions and boundary points. Differential Geometry, Proc. Symp. Pure Math. 54 (1993) 417-438. CrossRef
Taylor, J., Unique structure of solutions to a class of nonelliptic variational problems. Proc. Symp. Pure Math. 27 (1975) 419-427. CrossRef
Taylor, J. and Cahn, J.W., Catalog of saddle shaped surfaces in crystals. Acta Metall. 34 (1986) 1-12. CrossRef