Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T17:24:31.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Relaxation of singular functionals defined on Sobolev spaces

Published online by Cambridge University Press:  15 August 2002

Hafedh Ben Belgacem
Hafedh Ben Belgacem*
Affiliation:
Département de Mathématiques, Institut Préparatoire aux Études d'Ingénieurs de Sfax, Route Menzel Chaker - Km 0,5, BP. 805, 3000 Sfax, Tunisia; Fax: (00-216) 4. 246. 347. Max-Planck Institute for Mathematics in the Sciences, Inselstr. 22-26, 04103 Leipzig, Germany; [email protected].
Get access

Abstract

In this paper, we consider a Borel measurable function on the space of $\scriptstyle m\times n$ matrices $\scriptstyle f: M^{m\times n}\rightarrow \bar{\mathbb{R}}$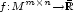 taking the value $ \scriptstyle +\infty$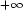, such that its rank-one-convex envelope $\scriptstyle Rf$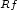 is finite and satisfies for some fixed $\scriptstyle p>1$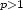: $$\scriptstyle -c_0\leq Rf(F)\leq c(1+\Vert F\Vert^p)\ \hbox{for all}\ F\in M^{m\times n},$$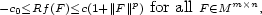 where $\scriptstyle c,c_0>0$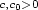. Let $\scriptstyle\O$ be a given regular bounded open domain of $\scriptstyle \mathbb{R}^n$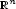. We define on $\scriptstyle W^{1,p}(\O;\mathbb{R}^m)$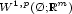 the functional $$\scriptstyle I(u)=\int_{\O}f(\nabla u(x))\ dx.$$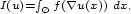 Then, under some technical restrictions on $\scriptstyle f$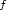, we show that the relaxed functional $\scriptstyle\bar I$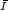 for the weak topology of $\scriptstyle W^{1,p}(\O;\mathbb{R}^m)$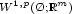 has the integral representation: $$\scriptstyle \bar I(u)=\int_{\O}Q[Rf](\nabla u(x))\ dx,$$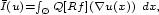 where for a given function $\scriptstyle g$, $\scriptstyle Qg$ 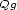denotes its quasiconvex envelope.

Keywords

Rank-one convexityquasiconvexityweak lower semicontinuity.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 5 , 2000 , pp. 71 - 85
Copyright
© EDP Sciences, SMAI, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E., Buttazzo, G. and Percivale, D., A variational definition of the strain energy for an elastic string. J. Elasticity 25 (1991) 137-148. CrossRef
Acerbi, E. and Fusco, N., Semicontinuity problems in the calculus of variations. Arch. Rational Mech. Anal. 86 (1984) 125-145. CrossRef
Anzellotti, G., Baldo, S. and Percivale, D., Dimension reduction in variational problems, asymptotic development in $\Gamma$ -convergence, and thin structures in elasticity. Asymptot. Anal. 9 (1994) 61-100.
Ball, J.M., Convexity conditions and existence theorems in nonlinear elasticity. Arch. Rational Mech. Anal. 63 (1977) 337-403. CrossRef
Ball, J.M. and Murat, F., W 1,p -quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58 (1984) 225-253. CrossRef
Ball, J.M. and James, R.D., Fine phase mixtures as minimizers of energy. Arch. Rational Mech. Anal. 100 (1987) 13-52. CrossRef
H. Ben Belgacem, Une méthode de $\Gamma$ -convergence pour un modèle de membrane non linéaire. C. R. Acad. Sci. Paris. Sér. I Math. (1996) 845-849.
H. Ben Belgacem, Modélisation de structures minces en élasticité non linéaire. Thèse de l'Université Pierre et Marie Curie, Paris (1996).
Bouchitté, G., Fonseca, I. and Malý, J., The effective bulk energy of the relaxed energy of multiple integrals below the growth exponent. Proc. Roy. Soc. Edinburgh Sect. A 128 (1998) 463-479. CrossRef
P.G. Ciarlet, Mathematical Elasticity. Vol. I: Three-dimensional Elasticity. North-Holland, Amesterdam (1988).
Dacorogna, B., Quasiconvexity and relaxation of non convex problems in the calculus of variations. J. Funct. Anal. 46 (1982) 102-118. CrossRef
Dacorogna, B., Remarques sur les notions de polyconvexité, quasiconvexité et convexité de rang 1. J. Math. Pures Appl. 64 (1985) 403-438.
B. Dacorogna, Direct Methods in the Calculus of Variations. Springer-Verlag, Berlin, Appl. Math. Sci. 78 (1989).
Dacorogna, B. and Marcellini, P., General existence theorems for Hamilton-Jacobi equations in the scalar and vectoriel cases. Acta Math. 178 (1997) 1-37. CrossRef
I. Ekeland and R. Temam, Analyse convexe et problèmes variationnels. Dunod, Paris (1974).
Fonseca, I., The lower quasiconvex envelope of the stored energy for an elastic crystal. J. Math. Pures Appl. 67 (1988) 175-195.
Fonseca, I., Variational techniques for problems in materials science. Progr. Nonlinear Differential Equations Appl. 25 (1996) 162-175.
Fonseca, I. and Malý, J., Relaxation of multiple integrals below the growth exponent. Ann. Inst. H. Poincaré 14 (1997) 309-338. CrossRef
Kohn, R.V. and Strang, G., Explicit relaxation of a variational problem in optimal design. Bull. Amer. Math. Soc. 9 (1983) 211-214. CrossRef
R.V. Kohn and G. Strang, Optimal design and relaxation of variational problems I, II and III. Comm. Pure Appl. Math. 39 (1986) 113-137, 139-182, 353-377.
H. Le Dret and A. Raoult, Le modèle de membrane non linéaire comme limite variationnelle de l'élasticité non linéaire tridimensionnelle. C. R. Acad. Sci. Paris Sér. I Math. (1993) 221-226.
Le Dret, H. and Raoult, A., The nonlinear membrane model as variational limit of three-dimensional nonlinear elasticity. J. Math. Pures Appl. 74 (1995) 549-578.
Marcellini, P., Approximation of quasiconvex functions and lower semicontinuity of multiple integrals. Manuscripta Math. 51 (1985) 1-28. CrossRef
Marcellini, P., On the definition and weak lower semicontinuity of certain quasiconvex integrals. Ann. Inst. H. Poincaré 3 (1986) 391-409. CrossRef
Morrey Jr, C.B.., Quasi-convexity and the lower semi-continuity of multiple integrals. Pacific J. Math. 2 (1952) 25-53. CrossRef
C.B. Morrey Jr., Multiple Integrals in the Calculus of Variations. Springer, Berlin (1966).
S. Müller, Variational models for microstructure and phase transitions, to appear in Proc. C.I.M.E. summer school ``Calculus of variations and geometric evolution problems''. Cetraro (1996).
R.W. Ogden, Large deformation isotropic elasticity: On the correlation of the theory and experiment for compressible rubberlike solids. Proc. Roy. Soc. London Ser. A 328 (1972).
E.T. Rockafellar, Convex Analysis. Princeton University Press (1970).
L. Tartar, Compensated Compactness and Applications to Partial Differential Equations, in Nonlinear Analysis and Mechanics, Heriot-Watt Symp. Vol. IV, R.J. Knops Ed. Pitman, London (1979).
V. Zhikov, Lavrentiev phenomenon and homogenization for some variational problems. C. R. Acad. Sci. Paris Sér. I Math. (1993) 435-439.