Article contents
The regularisation of the N-wellproblem by finite elements and by singular perturbation are scalingequivalentin two dimensions
Published online by Cambridge University Press: 24 June 2008
Abstract
Let $K:=SO\left(2\right)A_1\cup SO\left(2\right)A_2\dots SO\left(2\right)A_{N}$ 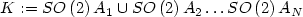 where $A_1,A_2,\dots, A_{N}$
where $A_1,A_2,\dots, A_{N}$ 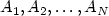 are matrices of non-zero determinant. Weestablish a sharp relation between the following two minimisationproblems in two dimensions. Firstly the N-well problem with surface energy. Let $p\in\left[1,2\right]$
are matrices of non-zero determinant. Weestablish a sharp relation between the following two minimisationproblems in two dimensions. Firstly the N-well problem with surface energy. Let $p\in\left[1,2\right]$  , $\Omega\subset \mathbb{R}^2$
, $\Omega\subset \mathbb{R}^2$ 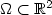 be a convex polytopal region. Define $$I^p_{\epsilon}\left(u\right)=\int_{\Omega} d^p\left(Du\left(z\right),K\right)+\epsilon\left|D^2u\left(z\right)\right|^2 {\rm d}L^2 z$$
be a convex polytopal region. Define $$I^p_{\epsilon}\left(u\right)=\int_{\Omega} d^p\left(Du\left(z\right),K\right)+\epsilon\left|D^2u\left(z\right)\right|^2 {\rm d}L^2 z$$  and let A F denote the subspace of functions in $W^{2,2}\left(\Omega\right)$
and let A F denote the subspace of functions in $W^{2,2}\left(\Omega\right)$ 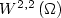 that satisfy the affine boundary conditionDu=F on $\partial \Omega$
that satisfy the affine boundary conditionDu=F on $\partial \Omega$ 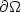 (in the sense of trace), where $F\not\inK$
(in the sense of trace), where $F\not\inK$ 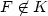 . We consider the scaling (with respect to ϵ) of $$m^p_{\epsilon}:=\inf_{u\in A_F} I^p_{\epsilon}\left(u\right).$$
. We consider the scaling (with respect to ϵ) of $$m^p_{\epsilon}:=\inf_{u\in A_F} I^p_{\epsilon}\left(u\right).$$ 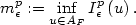 Secondly the finite element approximation to the N-well problemwithout surface energy. We will show there exists a space of functions $\mathcal{D}_F^{h}$
Secondly the finite element approximation to the N-well problemwithout surface energy. We will show there exists a space of functions $\mathcal{D}_F^{h}$ 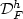 whereeach function $v\in \mathcal{D}_F^{h}$
whereeach function $v\in \mathcal{D}_F^{h}$ 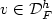 is piecewise affine on a regular(non-degenerate) h-triangulation and satisfies the affine boundarycondition v=lF on $\partial \Omega$
is piecewise affine on a regular(non-degenerate) h-triangulation and satisfies the affine boundarycondition v=lF on $\partial \Omega$ 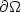 (where l F is affine with $Dl_F=F$
(where l F is affine with $Dl_F=F$ 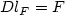 ) such that for $$\alpha_p\left(h\right):=\inf_{v\in \mathcal{D}_F^{h}}\int_{\Omega}d^p\left(Dv\left(z\right),K\right) {\rm d}L^2 z$$
) such that for $$\alpha_p\left(h\right):=\inf_{v\in \mathcal{D}_F^{h}}\int_{\Omega}d^p\left(Dv\left(z\right),K\right) {\rm d}L^2 z$$ 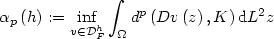 there exists positive constants $\mathcal{C}_1<1<\mathcal{C}_2$
there exists positive constants $\mathcal{C}_1<1<\mathcal{C}_2$ 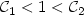 (depending on $A_1,\dots, A_{N}$
(depending on $A_1,\dots, A_{N}$  , p) for which the following holds true $$\mathcal{C}_1\alpha_p\left(\sqrt{\epsilon}\right)\leq m^p_{\epsilon}\leq\mathcal{C}_2\alpha_p\left(\sqrt{\epsilon}\right) \text{ for all }\epsilon>0.$$
, p) for which the following holds true $$\mathcal{C}_1\alpha_p\left(\sqrt{\epsilon}\right)\leq m^p_{\epsilon}\leq\mathcal{C}_2\alpha_p\left(\sqrt{\epsilon}\right) \text{ for all }\epsilon>0.$$ 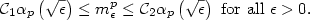
Keywords
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 15 , Issue 2 , April 2009 , pp. 322 - 366
- Copyright
- © EDP Sciences, SMAI, 2008
References
- 4
- Cited by


