Reachability of nonnegative equilibrium statesfor the semilinear vibrating string by varying its axial load and the gain of damping

Abstract

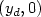We show that the set of nonnegative equilibrium-like states, namely, like $ (y_d, 0) $ of the semilinear vibrating string that can be reached from any non-zero initial state $ (y_0, y_1) \in H^1_0 (0,1) \times L^2 (0,1)$ 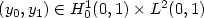, by varying its axial load and the gain of damping, is dense in the “nonnegative” part of the subspace $ L^2 (0,1) \times \{0\} $ 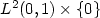of $ L^2 (0,1) \times H^{-1} (0,1)$ 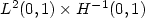. Our main results deal with nonlinear terms which admit at most the linear growth at infinity in $ \; y \; $ 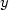and satisfy certain restriction on their total impact on (0,∞) with respect to the time-variable.