Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Van Heerden, Francois A.
2003.
Multiple solutions for a Schrödinger type equation with an asymptotically linear term.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 55,
Issue. 6,
p.
739.
Liu, Zhaoli
van Heerden, Francois A.
and
Wang, Zhi-Qiang
2005.
Nodal type bound states of Schrödinger equations via invariant set and minimax methods.
Journal of Differential Equations,
Vol. 214,
Issue. 2,
p.
358.
Stuart, Charles A.
and
Zhou, Huan-Song
2005.
Axisymmetric TE-Modes in a Self-focusing Dielectric.
SIAM Journal on Mathematical Analysis,
Vol. 37,
Issue. 1,
p.
218.
Liu, Zhaoli
Su, Jiabao
and
Weth, Tobias
2006.
Compactness results for Schrödinger equations with asymptotically linear terms.
Journal of Differential Equations,
Vol. 231,
Issue. 2,
p.
501.
Maia, L.A.
Montefusco, E.
and
Pellacci, B.
2006.
Positive solutions for a weakly coupled nonlinear Schrödinger system.
Journal of Differential Equations,
Vol. 229,
Issue. 2,
p.
743.
Ding, Yanheng
and
Jeanjean, Louis
2007.
Homoclinic orbits for a nonperiodic Hamiltonian system.
Journal of Differential Equations,
Vol. 237,
Issue. 2,
p.
473.
Watanabe, Tatsuya
2007.
On exterior Neumann problems with an asymptotically linear nonlinearity.
Journal of Differential Equations,
Vol. 240,
Issue. 1,
p.
1.
Huang, Yisheng
and
Wang, Feizhi
2008.
On a class of Schrödinger equations in with indefinite linear part.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 69,
Issue. 12,
p.
4504.
Liu, Chuangye
Wang, Zhengping
and
Zhou, Huan-Song
2008.
Asymptotically linear Schrödinger equation with potential vanishing at infinity.
Journal of Differential Equations,
Vol. 245,
Issue. 1,
p.
201.
Zhao, Fukun
Zhao, Leiga
and
Ding, Yanheng
2008.
Existence and multiplicity of solutions for a non-periodic Schrödinger equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 69,
Issue. 11,
p.
3671.
Wang, Zhengping
and
Zhou, Huan-Song
2009.
Positive solutions for a nonhomogeneous elliptic equation onRNwithout (AR) condition.
Journal of Mathematical Analysis and Applications,
Vol. 353,
Issue. 1,
p.
470.
STUART, C. A.
and
ZHOU, HUAN-SONG
2010.
EXISTENCE OF GUIDED CYLINDRICAL TM-MODES IN AN INHOMOGENEOUS SELF-FOCUSING DIELECTRIC.
Mathematical Models and Methods in Applied Sciences,
Vol. 20,
Issue. 09,
p.
1681.
Liu, Shibo
2010.
On ground states of superlinear p-Laplacian equations inRN.
Journal of Mathematical Analysis and Applications,
Vol. 361,
Issue. 1,
p.
48.
Alves, Claudianor O.
and
Liu, Shibo
2010.
On superlinearp(x)-Laplacian equations inRN.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 73,
Issue. 8,
p.
2566.
Sirakov, Boyan
2010.
Solvability of Uniformly Elliptic Fully Nonlinear PDE.
Archive for Rational Mechanics and Analysis,
Vol. 195,
Issue. 2,
p.
579.
Wang, Li
2011.
Positive Solutions to the Nonhomogenous <i>p</i>-Laplacian Problem with Nonlinearity Asymptotic to <i>u<sup>p</i>-1</sup>at Infinity in R<i><sup>N</sup></i>.
Applied Mathematics,
Vol. 02,
Issue. 09,
p.
1068.
Liu, Xiangqing
and
Liu, Jiaquan
2011.
On a boundary value problem in the half-space.
Journal of Differential Equations,
Vol. 250,
Issue. 4,
p.
2099.
Peng, Chaoquan
2011.
Asymptotically linear elliptic systems inRN.
Journal of Mathematical Analysis and Applications,
Vol. 380,
Issue. 2,
p.
540.
Guo, Yuxia
and
Liu, Xiangqing
2012.
A multiple critical points theorem and applications to quasilinear boundary value problems in.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 9,
p.
3787.
Massar, M.
Tsouli, N.
and
Hamydy, A.
2012.
Existence of weak solutions for a quasilinear equation inRN.
Journal of Mathematical Analysis and Applications,
Vol. 395,
Issue. 2,
p.
673.
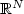 autonomous at infinity
autonomous at infinity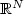 . The main
difficulties to overcome are the lack of a priori bounds for
Palais–Smale sequences and a lack of compactness as the domain is
unbounded. For the first one we make use of techniques introduced
by Lions in his work on concentration compactness. For the
second we show how the fact that the “Problem at infinity” is
autonomous, in contrast to just periodic, can be used in order to
regain compactness.
. The main
difficulties to overcome are the lack of a priori bounds for
Palais–Smale sequences and a lack of compactness as the domain is
unbounded. For the first one we make use of techniques introduced
by Lions in his work on concentration compactness. For the
second we show how the fact that the “Problem at infinity” is
autonomous, in contrast to just periodic, can be used in order to
regain compactness.