On the L^p-stabilization of the double integrator subject to input saturation

Abstract

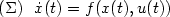We consider a finite-dimensional control system $(\Sigma)\ \ \dot x(t)=f(x(t),u(t))$, such that there exists a feedback stabilizer k that renders $\dot x=f(x,k(x))$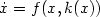 globally asymptotically stable. Moreover, for (H,p,q) with H an output map and $1\leq p\leq q\leq \infty$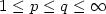, we assume that there exists a ${\cal {K}}_{\infty}$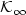-function α such that $\|H(x_u)\|_q\leq \alpha(\|u\|_p)$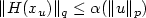, where x_u is the maximal solution of $(\Sigma)_k \ \ \dot x(t)=f(x(t),k(x(t))+u(t))$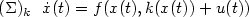, corresponding to u and to the initial condition x(0)=0. Then, the gain function $G_{(H,p,q)}$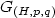 of (H,p,q) given by 14.5cm $$ G_{(H,p,q)}(X)\stackrel{\rm def}{=}\sup_{\|u\|_p=X}\|H(x_u)\|_q, $$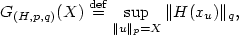 is well-defined. 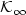We call profile of k for (H,p,q) any ${\cal {K}}_{\infty}$-function which is of the same order of magnitude as $G_{(H,p,q)}$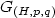. For the double integrator subject to input saturation and stabilized by $k_L(x)=-(1\ 1)^Tx$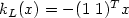, we determine the profiles corresponding to the main output maps. In particular, if $\sigma_0$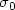 is used to denote the standard saturation function, we show that the L₂-gain from the output of the saturation nonlinearity to u of the system $\ddot x=\sigma_0(-x-\dot x+u)$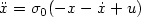 with $x(0)= \dot x(0)=0$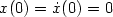, is finite. We also provide a class of feedback stabilizers k_F that have a linear profile for (x,p,p), $1\leq p\leq \infty$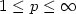. For instance, we show that the L₂-gains from x and $\dot x$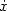 to u of the system $\ddot x=\sigma_0(-x-\dot x-(\dot x)^3+u)$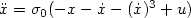 with $x(0)= \dot x(0)=0$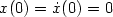, are finite.