Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T10:30:02.011Z Has data issue: false hasContentIssue false
  • English
  • Français

On the lower semicontinuous quasiconvex envelope for unbounded integrands (I)

Published online by Cambridge University Press:  23 January 2009

Marcus Wagner
Marcus Wagner*
Affiliation:
Brandenburg University of Technology, Cottbus; Department of Mathematics, P.O.B. 10 13 44, 03013 Cottbus, Germany. e-mail: [email protected]
Get access

Abstract

Motivated by the study of multidimensional control problems of Dieudonné-Rashevsky type, we raise the question how to understand to notion of quasiconvexity for a continuous function f with a convex body K $\subset \mathbb{R}^{nm}$ 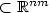instead of the whole space $\mathbb{R}^{nm}$ 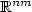as the range of definition. In the present paper, we trace the consequences of an infinite extension of f outside K, and thus study quasiconvex functions which are allowed to take the value +∞. As an appropriate envelope, we introduce and investigate the lower semicontinuous quasiconvex envelope $f^{(qc)} (v) = {\rm sup} \{ \,g(v)\, \vert \,g : \mathbb{R}^{nm} \rightarrow \mathbb{R} \cup \{ + \infty \}$ 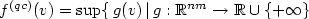quasiconvex and lower semicontinuous, $g(v) \leq f(v) \,\,\,\,\forall v \in \mathbb{R}^{nm}\,\}.$ 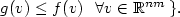Our main result is a representation theorem for $f^{({\it qc})}$ 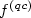which generalizes Dacorogna's well-known theorem on the representation of the quasiconvex envelope of a finite function. The paper will be completed by the calculation of $f^{({\it qc})}$ 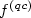in two examples.


Keywords

Unbounded functionquasiconvex functionquasiconvex envelopeMorrey's integral inequalityrepresentation theorem
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 15 , Issue 1 , January 2009 , pp. 68 - 101
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrejewa, J.A. and Klötzler, R., Zur analytischen Lösung geometrischer Optimierungsaufgaben mittels Dualität bei Steuerungsproblemen. Teil I. Z. Angew. Math. Mech. 64 (1984) 35–44. CrossRef
Andrejewa, J.A. and Klötzler, R., Zur analytischen Lösung geometrischer Optimierungsaufgaben mittels Dualität bei Steuerungsproblemen. Teil II. Z. Angew. Math. Mech. 64 (1984) 147–153. CrossRef
G. Aubert and P. Kornprobst, Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations. 2nd Edn., Springer, New York etc. (2006).
J.M. Ball and F. Murat, $W^{1,p}$ -quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58 (1984) 225–253.
A. Brøndsted, An Introduction to Convex Polytopes. Springer, New York - Heidelberg - Berlin (1983).
C. Brune, H. Maurer and M. Wagner, Edge detection within optical flow via multidimensional control. BTU Cottbus, Preprint-Reihe Mathematik, Preprint Nr. M-02/2008 (submitted).
C. Carathéodory, Vorlesungen über reelle Funktionen. 3rd Edn., Chelsea, New York (1968).
Casadio Tarabusi, E., An algebraic characterization of quasi-convex functions. Ricerche di Mat. 42 (1993) 11–24.
F.H. Clarke, Optimization and Nonsmooth Analysis. 2nd Edn., SIAM, Philadelphia (1990).
L. Collatz and W. Wetterling, Optimierungsaufgaben, 2nd Edn., Heidelberger Taschenbücher 15. Springer, Berlin - Heidelberg - New York (1971).
Dacorogna, B., Quasiconvexity and relaxation of nonconvex problems in the calculus of variations. J. Funct. Anal. 46 (1982) 102–118. CrossRef
B. Dacorogna, Direct Methods in the Calculus of Variations. 2nd Edn., Springer, New York etc. (2008).
Dacorogna, B. and Fusco, N., Semi-continuité des fonctionnelles avec contraintes du type “ $\hbox{\rm det}\, \nabla u > 0$ ". Boll. Un. Mat. Ital. B (6) 4 (1985) 179–189.
Dacorogna, B. and Marcellini, P., General existence theorems for Hamilton-Jacobi equations in the scalar and vectorial case. Acta Math. 178 (1997) 1–37. CrossRef
B. Dacorogna and P. Marcellini, Cauchy-Dirichlet problem for first order nonlinear systems. J. Funct. Anal. 152 (1998) 404–446.
B. Dacorogna and P. Marcellini, Implicit Partial Differential Equations. Birkhäuser, Boston - Basel - Berlin (1999).
B. Dacorogna and A.M. Ribeiro, On some definitions and properties of generalized convex sets arising in the calculus of variations, in Recent Advances on Elliptic and Parabolic Issues, M. Chipot and H. Ninomiya Eds., Proceedings of the 2004 Swiss-Japanese Seminar: Zurich, Switzerland, 6–10 December 2004, World Scientific, Singapore (2006) 103–128.
De Arcangelis, R. and Zappale, E., The relaxation of some classes of variational integrals with pointwise continuous-type gradient constraints. Appl. Math. Optim. 51 (2005) 251–257.
De Arcangelis, R., Monsurrò, S. and Zappale, E., On the relaxation and the Lavrentieff phenomenon for variational integrals with pointwise measurable gradient constraints. Calc. Var. Partial Differential Equations 21 (2004) 357–400. CrossRef
I. Ekeland and R. Témam, Convex Analysis and Variational Problems. 2nd Edn., SIAM, Philadelphia (1999).
J. Elstrodt, Maß- und Integrationstheorie. Springer, New York - Heidelberg - Berlin (1996).
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions. CRC Press, Boca Raton etc. (1992).
A.D. Ioffe and V.M. Tichomirow, Theorie der Extremalaufgaben. VEB Deutscher Verlag der Wissenschaften, Berlin (1979).
Kawohl, B., From Mumford-Shah to Perona-Malik in image processing. Math. Meth. Appl. Sci. 27 (2004) 1803–1814.
Kinderlehrer, D. and Pedregal, P., Characterizations of Young measures generated by gradients. Arch. Rat. Mech. Anal. 115 (1991) 329–365. CrossRef
Kristensen, J., On the non-locality of quasiconvexity. Ann. Inst. H. Poincaré Anal. Non Linéaire 16 (1999) 1–13. CrossRef
Kruskal, J.B., Two convex counterexamples: A discontinuous envelope function and a nondifferentiable nearest-point mapping. Proc. Amer. Math. Soc. 23 (1969) 697–703.
Kružík, M., Bauer's maximum principle and hulls of sets. Calc. Var. Partial Differential Equations 11 (2000) 321–332.
M. Kružík, Quasiconvex extreme points of convex sets, in Elliptic and Parabolic Problems, J. Bemelmans, B. Brighi, A. Brillard, M. Chipot, F. Conrad, I. Shafrir, V. Valente and G. Vergara-Caffarelli Eds., World Scientific Publishing, River Edge (2002) 145–151.
K.A. Lur'e, Hayka, Moscow (1975).
Morrey, C.B., Quasi-convexity and the lower semicontinuity of multiple integrals. Pacific J. Math. 2 (1952) 25–53. CrossRef
Pickenhain, S. and Wagner, M., Piecewise continuous controls in Dieudonné-Rashevsky type problems. J. Optim. Theory Appl. 127 (2005) 145–163. CrossRef
R.T. Rockafellar, Convex Analysis. 2nd Edn., Princeton University Press, Princeton (1972).
R.T. Rockafellar and R.J.-B. Wets, Variational Analysis, Grundlehren 317. Springer, Berlin etc. (1998).
R. Schneider, Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, Cambridge (1993).
Schulz, K. and Schwartz, B., Finite extensions of convex functions. Math. Operationsforschung Statist. Ser. Optimization 10 (1979) 501–509. CrossRef
Šverák, V., Rank-one convexity does not imply quasiconvexity. Proc. Roy. Soc. Edinburgh Ser. A 120 (1992) 185–189. CrossRef
Ting, T.W., Elastic-plastic torsion of convex cylindrical bars. J. Math. Mech. 19 (1969) 531–551.
Ting, T.W., Elastic-plastic torsion problem III. Arch. Rat. Mech. Anal. 34 (1969) 228–244.
M. Wagner, Erweiterungen des mehrdimensionalen Pontrjaginschen Maximumprinzips auf meßbare und beschränkte sowie distributionelle Steuerungen. Ph.D. thesis, Universität Leipzig, Germany (1996).
M. Wagner, Nonconvex relaxation properties of multidimensional control problems, in Recent Advances in Optimization, A. Seeger Ed., Lecture Notes in Economics and Mathematical Systems 563, Springer, Berlin etc. (2006) 233–250.
M. Wagner, Mehrdimensionale Steuerungsprobleme mit quasikonvexen Integranden. Habilitation thesis, Brandenburgische Technische Universität Cottbus, Cottbus, Germany (2006).
M. Wagner, Pontryagin's maximum principle for multidimensional control problems in image processing. J. Optim. Theory Appl. (to appear).
Zhang, K., On the structure of quasiconvex hulls. Ann. Inst. H. Poincaré Anal. Non Linéaire 15 (1998) 663–686. CrossRef
Zhang, K., On the quasiconvex exposed points. ESAIM: COCV 6 (2001) 1–19 (electronic). CrossRef