Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T21:37:10.556Z Has data issue: false hasContentIssue false
  • English
  • Français

On the curvature and torsion effects inone dimensional waveguides

Published online by Cambridge University Press:  05 September 2007

Guy Bouchitté ,
M. Luísa Mascarenhas  and
Luís Trabucho
Guy Bouchitté
Affiliation:
Département de Mathématiques, Université du Sud-Toulon-Var, BP 132, 83957 La Garde Cedex, France; [email protected]
M. Luísa Mascarenhas
Affiliation:
Departamento de Matemática da F.C.T.-U.N.L. e C.M.A.-U.N.L., Quinta da Torre, 2829-516 Caparica, Portugal; [email protected]
Luís Trabucho
Affiliation:
Departamento de Matemática da F.C.-U.L. e C.M.A.F.-U.L., Av. Prof. Gama Pinto 2, 1649-003 Lisboa, Portugal; [email protected]
Get access

Abstract

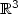We consider the Laplace operator in a thin tube of ${\mathbb R}^3$ with a Dirichlet condition on its boundary. We study asymptotically the spectrum ofsuch an operator as the thickness of the tube's cross section goes to zero. In particular weanalyse how the energy levels depend simultaneously on the curvature of the tube's central axisand on the rotation of the cross section with respect to the Frenet frame. The main argument is aΓ-convergence theorem for a suitable sequence of quadratic energies.

Keywords

Dimension reductionΓ-convergencecurvature and torsionwaveguides
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 4 , October 2007 , pp. 793 - 808
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allaire, G. and Conca, C., Bloch wave homogenization and spectral asymptotic analysis. J. Math. Pures Appl. 77 (1998) 153–208. CrossRef
Chenaud, B., Duclos, P., Freitas, P. and Krejčiřík, D., Geometrically induced discrete specrtum in curved tubes. Differ. Geometry Appl. 23 (2005) 95–105. CrossRef
C. Conca, J. Planchard and M. Vanninathan, Fluids and periodic structures, Research in Applied Mathematics 38. Masson, Paris (1995).
G. Dal Maso, An Introduction to Γ -Convergence. Birkhäuser, Boston (1993).
Duclos, P. and Exner, P., Curvature-induced bounds states in quantum waveguides in two and tree dimensions. Rev. Math. Phys. 7 (1995) 73–102. CrossRef
V. Jikov, S.M. Kozlov and O.A. Oleinik, Homogenization of Differential Operators and Integral Equations. Springer-Verlag, Berlin (1994).
P. Kuchment, On some spectral problems of mathematical physics. Partial differential equations and inverse problems., Contemp. Math. 362. Amer. Math. Soc., Providence, RI (2004) 241–276.
Rubinstein, J., Schatzman, M., Variational problems on multiply connected thin strips. II. Convergence of the Ginzburg-Landau functional. Arch. Ration. Mech. Anal. 160 (2001) 309–324. CrossRef
Vanninathan, M., Homogenization of eigenvalue problems in perforated domains. Proc. Indian Acad. Sci. Math. Sci. 90 (1981) 239–271. CrossRef