Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T10:28:18.509Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Volume Constrained Variational Problem in SBV²(Ω): Part I

Published online by Cambridge University Press:  15 September 2002

Ana Cristina Barroso  and
José Matias
Ana Cristina Barroso
Affiliation:
CMAF, Universidade de Lisboa, Av. Prof. Gama Pinto, 2, 1649-003 Lisboa, Portugal and Departamento de Matemática, Faculdade de Ciências, Universidade de Lisboa, 1749-016 Lisboa, Portugal; [email protected].
José Matias
Affiliation:
Departamento de Matemática, Instituto Superior Técnico, Av. Rovisco Pais, 1, 1049-001 Lisboa, Portugal; [email protected].
Get access

Abstract

We consider the problem of minimizing the energy $$ E(u):= \int_{\Omega}|\nabla u(x)|^2 \, {\rm d}x + \int_{S_u \cap \Omega}\left (1 + |[u](x)|\right) \, {\rm d}H^{N - 1}(x)$$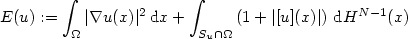 among all functions u ∈ SBV²(Ω) for which two level sets $\{u = l_i\}$ 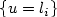have prescribed Lebesgue measure $\alpha_i$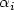. Subject to this volume constraint the existence of minimizers for E(.) is proved and the asymptotic behaviour of the solutions is investigated.

Keywords

Special functions of bounded variationlevel setslower semicontinuityΓ-limit.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 7 , 2002 , pp. 223 - 237
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

L. Ambrosio, A compactness theorem for a special class of functions of bounded variation. Boll. Un. Mat. Ital. 3-B (1989) 857-881.
Ambrosio, L., Fonseca, I., Marcellini, P. and Tartar, L., On a volume constrained variational problem. Arch. Rat. Mech. Anal. 149 (1999) 23-47. CrossRef
Aguilera, N., Alt, H.W. and Caffarelli, L.A., An optimization problem with volume constraint. SIAM J. Control Optim. 24 (1986) 191-198. CrossRef
Alt, H.W. and Caffarelli, L.A., Existence and regularity for a minimum problem with free boundary. J. Reine Angew. Math. 325 (1981) 105-144.
A. Braides and V. Chiadò-Piat, Integral representation results for functionals defined on $SBV(\Omega; {\mathbb R}^m)$ . J. Math. Pures Appl. 75 (1996) 595-626.
Congedo, G. and Tamanini, L., On the existence of solutions to a problem in multidimensional segmentation. Ann. Inst. H. Poincaré Anal. Non Linéaire 2 (1991) 175-195. CrossRef
De Giorgi, E. and Ambrosio, L., Un nuovo tipo di funzionale del calcolo delle variazioni. Atti Accad. Naz. Lincei 82 (1988) 199-210.
G. Dal Maso, An Introduction to Γ-convergence. Birkhäuser (1993).
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions. CRC Press, Stud. Adv. Math. (1992).
E. Giusti, Minimal Surfaces and Functions of Bounded Variation. Birkhäuser (1984).
Gurtin, M.E., Polignone, D. and Vinals, J., Two-phase binary fluids and immiscible fluids described by an order parameter. Math. Models Methods Appl. Sci. 6 (1996) 815-831. CrossRef
Tilli, P., On a constrained variational problem with an arbitrary number of free boundaries. Interf. Free Boundaries 2 (2000) 201-212. CrossRef
W. Ziemer, Weakly Differentiable Functions. Springer-Verlag (1989).