Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T04:57:41.261Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study of a new global minimizerfor the Mumford-Shah functional in R3

Published online by Cambridge University Press:  20 June 2007

Benoît Merlet
Benoît Merlet*
Affiliation:
Université Paris Nord - Institut Galillée, LAGA (Laboratoire d'Analyse Géométrie et Applications), Avenue J.B. Clément, 93430 Villetaneuse, France; [email protected]
Get access

Abstract

In [Progress Math.233 (2005)], David suggested the existence of a new type of global minimizers for the Mumford-Shah functional in $\mathbf{R}^3$ 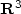. The singular set of such a new minimizer belongs to a three parameters family of sets $(0<\delta_1,\delta_2,\delta_3<\pi)$ 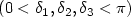. We first derive necessary conditions satisfied by global minimizers of this family. Then we are led to study the first eigenvectors of the Laplace-Beltrami operator with Neumann boundary conditions on subdomains of $\mathbf{S}^2$ 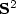with three reentrant corners. The necessary conditions are constraints on the eigenvalue and on the ratios between the three singular coefficients of the associated eigenvector. We use numerical methods (Singular Functions Method and Moussaoui's extraction formula) to compute the eigenvalues and the singular coefficients. We conclude that there is no $(\delta_1,\delta_2,\delta_3)$ 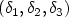for which the necessary conditions are satisfied and this shows that the hypothesis was wrong.

Keywords

Mumford-Shah functionalnumerical analysisboundary value problems for second-orderelliptic equations in domains with corners
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 3 , July 2007 , pp. 553 - 569
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M. Amara and M.-A. Moussaoui, Approximation of solutions and singularities coefficients for an elliptic problem in a plane polygonal domain. Note Technique, E.N.S. Lyon (1989).
Bonnet, A., On the regularity of edges in image segmentation. Ann. Inst. H. Poincaré Anal. Non Linéaire 13 (1996) 485–528. CrossRef
Bourlard, M., Dauge, M., Lubuma, M.S and Nicaise, S., Coefficients of the singularities for elliptic boundary value problems on domains with conical points. III. Finite element methods on polygonal domains. SIAM J. Numer. Anal. 29 (1992) 136–155. CrossRef
Ciarlet, P., Jr. and J. He, The singular complement method for 2d scalar problems. C. R. Math. Acad. Sci. Paris 336 (2003) 353–358. CrossRef
M. Dauge, Elliptic boundary value problems on corner domains, Lect. Notes Math. 1341. Smoothness and asymptotics of solutions. Springer-Verlag, Berlin (1988).
Dauge, M., Nicaise, S., Bourlard, M. and Lubuma, M.S., Coefficients des singularités pour des problèmes aux limites elliptiques sur un domaine à points coniques. I. Résultats généraux pour le problème de Dirichlet. RAIRO Modél. Math. Anal. Numér. 24 (1990) 27–52. CrossRef
Dauge, M., Nicaise, S., Bourlard, M. and Lubuma, M.S., Coefficients des singularités pour des problèmes aux limites elliptiques sur un domaine à points coniques. II. Quelques opérateurs particuliers. RAIRO Modél. Math. Anal. Numér. 24 (1990) 343–367. CrossRef
G. David, Singular sets of minimizers for the Mumford-Shah functional. Progress Math. 233, Birkhäuser Verlag, Basel (2005).
De Giorgi, E., Carriero, M. and Leaci, A., Existence theorem for a minimum problem with free discontinuity set. Arch. Rational. Mech. Anal. 108 (1989) 195–218. CrossRef
A. Ern and J.-L Guermond, Éléments finis: théorie, applications, mise en œ uvre. Math. Appl. 36, Springer-Verlag, Berlin (2002).
P. Grisvard, Singularities in boundary value problems, Recherches Math. Appl. 22 . Masson, Paris (1992).
Kondrat'ev, V.A., Boundary value problems for elliptic equations in domains with conical or angular points. Trudy Moskov. Mat. Obšč. 16 (1967) 209–292.
M.-A. Moussaoui, Sur l'approximation des solutions du problème de Dirichlet dans un ouvert avec coins, in Singularities and constructive methods for their treatment (Oberwolfach, 1983). Lect. Notes Math. 1121, Springer, Berlin (1985) 199–206.
Mumford, D. and Shah, J., Optimal approximations by piecewise smooth functions and associated variational problems. Comm. Pure Appl. Math. 42 (1989) 577–685. CrossRef