Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-30T19:30:44.387Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on convergence of low energy critical pointsof nonlinear elasticity functionals,for thin shells of arbitrary geometry

Published online by Cambridge University Press:  24 March 2010

Marta Lewicka
Marta Lewicka*
Affiliation:
Marta Lewicka, University of Minnesota, Department of Mathematics, 206 Church St. S.E., Minneapolis, MN 55455, USA. [email protected]
Get access

Abstract

We prove that the critical points of the 3d nonlinear elasticity functionalon shells of small thickness h and around the mid-surface S of arbitrary geometry, converge as h → 0to the critical points of the vonKármán functional on S, recently proposed in [Lewicka et al., Ann. Scuola Norm. Sup. Pisa Cl. Sci. (to appear)].This result extends the statement in [Müller and Pakzad, Comm. Part. Differ. Equ. 33 (2008) 1018–1032], derived for the case of plates when $S\subset\mathbb{R}^2$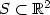.The convergence holds provided the elastic energies of the 3d deformations scale like h4 and the external body forces scale like h3.

Keywords

Shell theoriesnonlinear elasticityGamma convergencecalculus of variations
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 2 , April 2011 , pp. 493 - 505
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

J.M. Ball, Some open problems in elasticity, in Geometry, mechanics, and dynamics, Springer, New York, USA (2002) 3–59.
P.G. Ciarlet, Mathematical Elasticity, Vol. 3: Theory of Shells. North-Holland, Amsterdam (2000).
G. Dal Maso, An introduction to Γ-convergence, Progress in Nonlinear Differential Equations and their Applications 8. Birkhäuser, USA (1993).
Friesecke, G., James, R. and Müller, S., A theorem on geometric rigidity and the derivation of nonlinear plate theory from three dimensional elasticity. Comm. Pure. Appl. Math. 55 (2002) 1461–1506. CrossRef
Friesecke, G., James, R. and Müller, S., A hierarchy of plate models derived from nonlinear elasticity by gamma-convergence. Arch. Ration. Mech. Anal. 180 (2006) 183–236. CrossRef
LeDret, H. and Raoult, A., The nonlinear membrane model as a variational limit of nonlinear three-dimensional elasticity. J. Math. Pures Appl. 73 (1995) 549–578.
M. Lewicka and M. Pakzad, The infinite hierarchy of elastic shell models: some recent results and a conjecture. Preprint (2009) http://arxiv.org/abs/0907.1585.
M. Lewicka, M.G. Mora and M.R. Pakzad, The matching property of infinitesimal isometries on elliptic surfaces and elasticity of thin shells. Preprint (2008) http://arxiv.org/abs/0811.2238.
M. Lewicka, M.G. Mora and M.R. Pakzad, A nonlinear theory for shells with slowly varying thickness. C. R. Acad. Sci. Paris, Sér. I 347 (2009) 211–216.
M. Lewicka, M.G. Mora and M.R. Pakzad, Shell theories arising as low energy Γ-limit of 3d nonlinear elasticity. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (to appear).
A.E.H. Love, A treatise on the mathematical theory of elasticity. 4th Edn., Cambridge University Press, Cambridge, UK (1927).
Mora, M.G. and Müller, S., Convergence of equilibria of three-dimensional thin elastic beams. Proc. Roy. Soc. Edinburgh Sect. A 138 (2008) 873–896. CrossRef
M.G. Mora and L. Scardia, Convergence of equilibria of thin elastic plates under physical growth conditions for the energy density. Preprint (2008).
Mora, M.G., Müller, S. and Schultz, M.G., Convergence of equilibria of planar thin elastic beams. Indiana Univ. Math. J. 56 (2007) 2413–2438.
Müller, S. and Pakzad, M.R., Convergence of equilibria of thin elastic plates – the von Kármán case. Comm. Part. Differ. Equ. 33 (2008) 1018–1032. CrossRef
M. Spivak, A Comprehensive Introduction to Differential Geometry, Vol. V. Second Edn., Publish or Perish Inc., Australia (1979).
T. von Kármán, Festigkeitsprobleme im Maschinenbau, in Encyclopädie der Mathematischen Wissenschaften IV. B.G. Teubner, Leipzig, Germany (1910) 311–385.