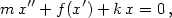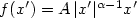Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Díaz, J.I.
2005.
Elliptic and Parabolic Problems.
Vol. 63,
Issue. ,
p.
217.
Díaz, J.I.
2005.
Nonlinear Elliptic and Parabolic Problems.
Vol. 64,
Issue. ,
p.
71.
Kouznetsov, D
Bisson, J-F
Li, J
and
Ueda, K
2007.
Self-pulsing laser as oscillator Toda: approximations through elementary functions.
Journal of Physics A: Mathematical and Theoretical,
Vol. 40,
Issue. 9,
p.
2107.
Besse, Christophe
Carles, Rémi
and
Ervedoza, Sylvain
2020.
A conservation law with spatially localized sublinear damping.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 37,
Issue. 1,
p.
13.