Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T21:14:05.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Multi-peak solutions for magnetic NLS equations without non-degeneracy conditions

Published online by Cambridge University Press:  20 August 2008

Silvia Cingolani ,
Louis Jeanjean  and
Simone Secchi
Silvia Cingolani
Affiliation:
Dipartimento di Matematica, Politecnico di Bari, via Orabona 4, 70125 Bari, Italy. [email protected]
Louis Jeanjean
Affiliation:
Équipe de Mathématiques (UMR CNRS 6623), 16 Route de Gray, 25030 Besançon, France. [email protected]
Simone Secchi
Affiliation:
Dipartimento di Matematica ed Applicazioni, Università di Milano-Bicocca, via Cozzi 53, 20125 Milano, Italy. [email protected]
Get access

Abstract

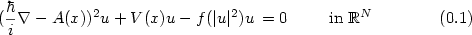In this work we consider the magnetic NLS equation $$ ( \frac{\hbar}{i} \nabla -A(x))^2 u + V(x)u - f(|u|^2)u \, = 0 \, \qquad \mbox{ in } \mathbb{R}^N\qquad\qquad(0.1)$$ where $N \geq 3$ , $A \colon \mathbb{R}^N \to \mathbb{R}^N$ 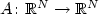is a magnetic potential,possibly unbounded, $V \colon \mathbb{R}^N \to \mathbb{R}$ is a multi-well electricpotential, which can vanish somewhere, f is a subcriticalnonlinear term. We prove the existence of a semiclassical multi-peaksolution $u\colon \mathbb{R}^N \to \mathbb{C}$ 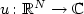to (0.1), under conditionson the nonlinearity which are nearly optimal.

Keywords

Nonlinear Schrödinger equationsmagnetic fieldsmulti-peaks
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 15 , Issue 3 , July 2009 , pp. 653 - 675
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosetti, A., Badiale, M. and Cingolani, S., Semiclassical states of nonlinear Schrödinger equations. Arch. Ration. Mech. Anal. 140 (1997) 285–300. CrossRef
Ambrosetti, A., Malchiodi, A. and Secchi, S., Multiplicity results for some nonlinear Schrödinger equations with potentials. Arch. Ration. Mech. Anal. 159 (2001) 253–271. CrossRef
Arioli, G. and Szulkin, A., A semilinear Schrödinger equations in the presence of a magnetic field. Arch. Ration. Mech. Anal. 170 (2003) 277–295. CrossRef
Barile, S., Cingolani, S. and Secchi, S., Single-peaks for a magnetic Schrödinger equation with critical growth. Adv. Diff. Equations 11 (2006) 1135–1166.
Bartsch, T., Dancer, E.N. and Peng, S., On multi-bump semi-classical bound states of nonlinear Schrödinger equations with electromagnetic fields. Adv. Diff. Equations 11 (2006) 781–812.
Berestycki, H. and Lions, P.L., Nonlinear scalar field equation I. Arch. Ration. Mech. Anal. 82 (1983) 313–346.
Byeon, J. and Jeanjean, L., Standing waves for nonlinear Schrödinger equations with a general nonlinearity. Arch. Ration. Mech. Anal. 185 (2007) 185–200. CrossRef
J. Byeon and L. Jeanjean, Erratum: Standing waves for nonlinear Schrödinger equations with a general nonlinearity. Arch. Ration. Mech. Anal. DOI 10.1007/s00205-006-0019-3.
Byeon, J. and Jeanjean, L., Multi-peak standing waves for nonlinear Schrödinger equations with a general nonlinearity. Discrete Cont. Dyn. Systems 19 (2007) 255–269.
Byeon, J. and Wang, Z.-Q., Standing waves with critical frequency for nonlinear Schrödinger equations. Arch. Rat. Mech. Anal. 165 (2002) 295–316. CrossRef
Byeon, J. and Wang, Z.-Q., Standing waves with critical frequency for nonlinear Schrödinger equations II. Calc. Var. Partial Differ. Equ. 18 (2003) 207–219. CrossRef
Byeon, J., Jeanjean, L. and Tanaka, K., Standing waves for nonlinear Schrödinger equations with a general nonlinearity: one and two dimensional cases. Comm. Partial Diff. Eq. 33 (2008) 1113–1136. CrossRef
Cao, D. and Noussair, E.-S., Multi-bump standing waves with a critical frequency for nonlinear Schrödinger equations. J. Diff. Eq. 203 (2004) 292–312. CrossRef
T. Cazenave, Semilinear Schrödinger equations, Courant Lecture Notes. AMS (2003).
Chabrowski, J. and Szulkin, A., On the Schrödinger equation involving a critical Sobolev exponent and magnetic field. Topol. Methods Nonlinear Anal. 25 (2005) 3–21. CrossRef
Cingolani, S., Semiclassical stationary states of nonlinear Schrödinger equations with an external magnetic field. J. Diff. Eq. 188 (2003) 52–79. CrossRef
Cingolani, S. and Lazzo, M., Multiple positive solutions to nonlinear Schrödinger equations with competing potential functions. J. Diff. Eq. 160 (2000) 118–138. CrossRef
Cingolani, S. and Nolasco, M., Multi-peaks periodic semiclassical states for a class of nonlinear Schrödinger equations. Proc. Royal Soc. Edinburgh 128 (1998) 1249–1260. CrossRef
Cingolani, S. and Secchi, S., Semiclassical limit for nonlinear Schrödinger equations with electromagnetic fields. J. Math. Anal. Appl. 275 (2002) 108–130. CrossRef
Cingolani, S. and Secchi, S., Semiclassical states for NLS equations with magnetic potentials having polynomial growths. J. Math. Phys. 46 (2005) 1–19. CrossRef
M. Clapp, R. Iturriaga and A. Szulkin, Periodic solutions to a nonlinear Schrödinger equations with periodic magnetic field. Preprint.
Coti-Zelati, V. and Rabinowitz, P.H., Homoclinic orbits for second order Hamiltonian systems possessing superquadratic potentials. J. Amer. Math. Soc. 4 (1991) 693–727. CrossRef
Coti-Zelati, V. and Rabinowitz, P.H., Homoclinic type solutions for a semilinear elliptic PDE on $\mathbb{R}^N$ . Comm. Pure Appl. Math. 45 (1992) 1217–1269.
Del Pino, M. and Felmer, P., Local mountain passes for semilinear elliptic problems in unbounded domains. Calc. Var. Partial Differ. Equ. 4 (1996) 121–137. CrossRef
Del Pino, M. and Felmer, P., Semi-classical states for nonlinear Schrödinger equations. J. Funct. Anal. 149 (1997) 245–265. CrossRef
Del Pino, M. and Felmer, P., Multi-peak bound states for nonlinear Schrödinger equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 15 (1998) 127–149. CrossRef
M.J. Esteban and P.L. Lions, Stationary solutions of nonlinear Schrödinger equations with an external magnetic field, in PDE and Calculus of Variations, in honor of E. De Giorgi, Birkhäuser (1990).
Floer, A. and Weinstein, A., Nonspreading wave packets for the cubic Schrödinger equation with a bounded potential. J. Funct. Anal. 69 (1986) 397–408. CrossRef
D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order, second edition, Grundlehren 224. Springer, Berlin, Heidelberg, New York and Tokyo (1983).
Gui, C., Existence of multi-bump solutions for nonlinear Schrödinger equations. Comm. Partial Diff. Eq. 21 (1996) 787–820. CrossRef
Hajaiej, H. and Stuart, C.A., On the variational approach to the stability of standing waves for the nonlinear Schrödinger equation. Advances Nonlinear Studies 4 (2004) 469–501. CrossRef
Jeanjean, L. and Tanaka, K., A remark on least energy solutions in $\mathbb{R}^N$ . Proc. Amer. Math. Soc. 131 (2003) 2399–2408. CrossRef
Jeanjean, L. and Tanaka, K., A note on a mountain pass characterization of least energy solutions. Advances Nonlinear Studies 3 (2003) 461–471. CrossRef
Jeanjean, L. and Tanaka, K., Singularly perturbed elliptic problems with superlinear or asympotically linear nonlinearities. Calc. Var. Partial Diff. Equ. 21 (2004) 287–318. CrossRef
Kurata, K., Existence and semi-classical limit of the least energy solution to a nonlinear Schrödinger equation with electromagnetic fields. Nonlinear Anal. 41 (2000) 763–778. CrossRef
On, Y.Y. Li a singularly perturbed elliptic equation. Adv. Diff. Equations 2 (1997) 955–980.
Lions, P.L., The concentration-compactness principle in the calculus of variations. The locally compact case. Part II. Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984) 223–283. CrossRef
Existence, Y.G. Oh of semiclassical bound states of nonlinear Schrödinger equations. Comm. Partial Diff. Eq. 13 (1988) 1499–1519.
M.H. Protter and H.F. Weinberger, Maximum Principles in Differential Equations. Springer-Verlag, New York, Berlin, Heidelberg and Tokyo (1984).
Rabinowitz, P., On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43 (1992) 270–291. CrossRef
M. Reed and B. Simon, Methods of Modern Mathematical Physics, Vol. II. Academic press, New York (1972).
Secchi, S. and Squassina, M., On the location of spikes for the Schrödinger equations with electromagnetic field. Commun. Contemp. Math. 7 (2005) 251–268. CrossRef
Strauss, W., Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55 (1977) 149–162. CrossRef
M. Struwe, Variational Methods, Application to Nonlinear Partial Differential Equations and Hamiltonian Systems. Springer-Verlag (1990).
Wang, X. and Zeng, B., On concentration of positive bound states of nonlinear Schrödinger equation with competing potential functions. SIAM J. Math. Anal. 28 (1997) 633–655. CrossRef