Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T05:13:22.055Z Has data issue: false hasContentIssue false
  • English
  • Français

The internal stabilization by noiseof the linearized Navier-Stokes equation*

Published online by Cambridge University Press:  30 October 2009

Viorel Barbu
Viorel Barbu*
Affiliation:
Al.I. Cuza University and Octav Mayer Institute of Mathematics of Romanian Academy, Iaşi, Romania. [email protected]
Get access

Abstract

One shows that the linearized Navier-Stokes equation in ${\mathcal{O}}{\subset} R^d,\;d \ge 2$ 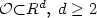, around an unstable equilibriumsolution is exponentially stabilizable in probability by aninternal noise controller $V(t,\xi)=\displaystyle\sum\limits_{i=1}^{N} V_i(t)\psi_i(\xi)\dot\beta_i(t)$ 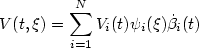, $\xi\in{\mathcal{O}}$ 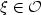, where $\{\beta_i\}^N_{i=1}$ 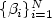areindependent Brownian motions in a probability space and $\{\psi_i\}^N_{i=1}$ 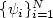is a system of functions on ${\mathcal{O}}$ withsupport in an arbitrary open subset ${\mathcal{O}}_0\subset {\mathcal{O}}$ 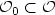. Thestochastic control input $\{V_i\}^N_{i=1}$ is found in feedbackform. One constructs also a tangential boundary noise controllerwhich exponentially stabilizes in probability the equilibriumsolution.

Keywords

Navier-Stokes equationfeedback controllerstochastic processStokes-Oseen operator
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 1 , January 2011 , pp. 117 - 130
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apleby, J.A.D., Mao, X. and Rodkina, A., Stochastic stabilization of functional differential equations. Syst. Control Lett. 54 (2005) 1069–1081. CrossRef
Apleby, J.A.D., Mao, X. and Rodkina, A., Stabilization and destabilization of nonlinear differential equations by noise. IEEE Trans. Automat. Contr. 53 (2008) 683–691. CrossRef
Arnold, L., Craul, H. and Wihstutz, V., Stabilization of linear systems by noise. SIAM J. Contr. Opt. 21 (1983) 451–461. CrossRef
Barbu, V., Feedback stabilization of Navier-Stokes equations. ESAIM: COCV 9 (2003) 197–205. CrossRef
Barbu, V. and Triggiani, R., Internal stabilization of Navier-Stokes equations with finite dimensional controllers. Indiana Univ. Math. J. 53 (2004) 1443–1494. CrossRef
V. Barbu, I. Lasiecka and R. Triggiani, Tangential boundary stabilization of Navier-Stokes equations, Memoires Amer. Math. Soc. AMS, USA (2006).
Caraballo, T., Liu, K. and Mao, X., On stabilization of partial differential equations by noise. Nagoya Math. J. 101 (2001) 155–170. CrossRef
Caraballo, T., Craul, H., Langa, J.A. and Robinson, J.C., Stabilization of linear PDEs by Stratonovich noise. Syst. Control Lett. 53 (2004) 41–50. CrossRef
Cerrai, S., Stabilization by noise for a class of stochastic reaction-diffusion equations. Prob. Th. Rel. Fields 133 (2000) 190–214. CrossRef
G. Da Prato, An Introduction to Infinite Dimensional Analysis. Springer-Verlag, Berlin, Germany (2006).
Ding, H., Krstic, M. and Williams, R.J., Stabilization of stochastic nonlinear systems driven by noise of unknown covariance. IEEE Trans. Automat. Contr. 46 (2001) 1237–1253. CrossRef
Duan, J. and Fursikov, A., Feedback stabilization for Oseen Fluid Equations. A stochastic approach. J. Math. Fluids Mech. 7 (2005) 574–610. CrossRef
A. Fursikov, Real processes of the 3-D Navier-Stokes systems and its feedback stabilization from the boundary, in AMS Translations, Partial Differential Equations, M. Vîshnik Seminar 206, M.S. Agranovic and M.A. Shubin Eds. (2002) 95–123.
Fursikov, A., Stabilization for the 3-D Navier-Stokes systems by feedback boundary control. Discrete Contin. Dyn. Syst. 10 (2004) 289-314. CrossRef
T. Kato, Perturbation Theory of Linear Operators. Springer-Verlag, New York, Berlin (1966).
Kuksin, S. and Shirikyan, A., Ergodicity for the randomly forced 2D Navier-Stokes equations. Math. Phys. Anal. Geom. 4 (2001) 147–195. CrossRef
T. Kurtz, Lectures on Stochastic Analysis. Lecture Notes Online, Wisconsin (2007), available at http://www.math.wisc.edu/~kurtz/735/main735.pdf.
R. Lipster and A.N. Shiraev, Theory of Martingals. Dordrecht, Kluwer (1989).
Mao, X.R., Stochastic stabilization and destabilization. Syst. Control Lett. 23 (2003) 279–290. CrossRef
Raymond, J.P., Feedback boundary stabilization of the two dimensional Navier-Stokes equations. SIAM J. Contr. Opt. 45 (2006) 790–828. CrossRef
Raymond, J.P., Feedback boundary stabilization of the three dimensional incompressible Navier-Stokes equations. J. Math. Pures Appl. 87 (2007) 627–669. CrossRef
Shirikyan, A., Exponential mixing 2D Navier-Stokes equations perturbed by an unbounded noise. J. Math. Fluids Mech. 6 (2004) 169–193. CrossRef