How to get a conservative well-posed linear system out of thin air. Part I. Well-posedness and energy balance

Abstract

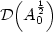Let A₀ be a possibly unbounded positive operator on the Hilbert space H, which is boundedly invertible. Let C₀ be a bounded operator from ${\cal D}\Big(A_0^{\frac{1}{2}}\Big)$ to another Hilbert space U. We prove that the system of equations $$\ddot z(t)+A_0 z(t) + {\frac{1}{2}}C_0^*C_0\dot z(t) =C_0^*u(t) $$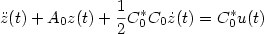$$y(t) =-C_0 \dot z(t)+u(t),$$ 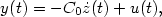determines a well-posed linear system with input u and output y. The state of this system is $$ x(t) = \left[\begin{matrix}\, z(t) \\ \dot z(t)\end{matrix}\right] \in {\cal D}\left(A_0^{\frac{1}{2}}\right)\times H = X , $$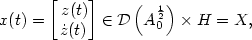 where X is the state space. Moreover, we have the energy identity $$ \|x(t)\|^2_X-\|x(0)\|_X^2 = \int_0^T\| u(t)\|^2_U {\rm d}t - \int_0^T \|y(t)\|_U^2 {\rm d}t. 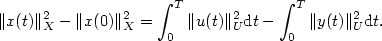$$ We show that the system described above is isomorphic to its dual, so that a similar energy identity holds also for the dual system and hence, the system is conservative. We derive various other properties of such systems and we give a relevant example: a wave equation on a bounded n-dimensional domain with boundary control and boundary observation on part of the boundary.