Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T21:21:03.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Homogenization of micromagnetics large bodies

Published online by Cambridge University Press:  15 March 2004

Giovanni Pisante
Giovanni Pisante*
Affiliation:
Dipartimento di Matematica e Applicazioni “R. Caccioppoli", Universitá degli Studi di Napoli “Federico II”, Italy. Département de Mathématique, E.P.F.L., Lausanne, Suisse; [email protected].; [email protected].
Get access

Abstract

A homogenization problem related to the micromagnetic energy functional is studied. In particular, the existence of the integral representation for the homogenized limit of a family of energies $$ \mathcal{E}_{\varepsilon}(m)=\int_{\Omega} \phi\left(x,\frac{x}{\varepsilon},m(x)\right)\,{\rm d}x-\int_{\Omega}h_e(x)\cdot m(x)\,{\rm d}x+\frac{1}{2}\int_{\mathbb R^3}|\nabla u(x)|^2\,{\rm d}x$$ 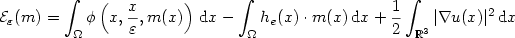of a large ferromagnetic body is obtained.

Keywords

MicromagneticshomogenizationΓ-convergence.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 10 , Issue 2 , April 2004 , pp. 295 - 314
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anzellotti, G., Baldo, S. and Visintin, A., Asymptotic behavior of the Landau-Lifshitz model of ferromagnetism. Appl. Math. Optim. 23 (1991) 171-192. CrossRef
Ball, J.M., Taheri, A. and Winter, M., Local minimizers in micromagnetics and related problems. Calc. Var. Partial Differ. Equ. 14 (2002) 1-27. CrossRef
A. Braides and A. Defranceschi, Homogenization of multiple integrals. The Clarendon Press Oxford University Press, New York, Oxford Lecture Ser. Math. Appl. 12 (1998).
Braides, A., Fonseca, I. and Leoni, G., A-quasiconvexity: relaxation and homogenization. ESAIM: COCV 5 (2000) 539-577 (electronic). CrossRef
Jr. Brown and W. Fuller, Micromagnetics. Interscience Publishers, John Wiley & Sons, New York, London (1963).
B. Dacorogna, Direct methods in the calculus of variations. Appl. Math. Sci. 78 (1989).
Dacorogna, B. and Fonseca, I., A-B quasiconvexity and implicit partial differential equations. Calc. Var. Partial Differ. Equ. 14 (2002) 115-149. CrossRef
G. Dal Maso, An introduction to $\Gamma$ -convergence. Birkhäuser Boston Inc., Boston, MA Prog. Nonlinear Differ. Equ. Appl. 8 (1993).
De Simone, A., Energy minimizers for large ferromagnetic bodies. Arch. Ration. Mech. Anal. 125 (1993) 99-143. CrossRef
De Simone, A., Hysteresis and imperfection sensitivity in small ferromagnetic particles. Meccanica 30 (1995) 591-603. Microstructure and phase transitions in solids (Udine, 1994). CrossRef
De, A. simone, R.V. Kohn, S. Müller and F. Otto, A reduced theory for thin-film micromagnetics. Commun. Pure Appl. Math. 55 (2002) 1408-1460.
De Simone, A., Müller, S., Kohn, R.V. and Otto, F., A compactness result in the gradient theory of phase transitions. Proc. R. Soc. Edinb. Sect. A 131 (2001) 833-844. CrossRef
I. Fonseca and G. Leoni, Relaxation results in micromagnetics. Ricerche Mat. 49 (2000) (suppl.) 269-304. Contributions in honor of the memory of Ennio De Giorgi (Italian).
James, R.D. and Kinderlehrer, D., Frustration in ferromagnetic materials. Contin. Mech. Thermodyn. 2 (1990) 215-239. CrossRef
L.D. Landau and E.M. Lifshits, Teoreticheskaya fizika. Tome VIII. “Nauka”, Moscow, third edition (1992). Elektrodinamika sploshnykh sred. [Electrodynamics of continuous media], with a preface by Lifshits and L.P. Pitaevskiĭ, edited and with a preface by Pitaevskiĭ.
L. Tartar, On mathematical tools for studying partial differential equations of continuum physics: H-measures and Young measures. Plenum, New York, in Developments in partial differential equations and applications to mathematical physics (Ferrara, 1991), (1992) 201-217.
Tartar, L., Beyond Young measures. Meccanica 30 (1995) 505-526. Microstructure and phase transitions in solids (Udine, 1994). CrossRef
Visintin, A., Landau-Lifshitz', On equations for ferromagnetism. Japan J. Appl. Math. 2 (1985) 69-84. CrossRef