Published online by Cambridge University Press: 11 October 2006
The energy in a square membrane Ω subject to constant viscous dampingon a subset $\omega\subset \Omega$  decays exponentially in timeas soon as ωsatisfies a geometrical condition known as the “Bardos-Lebeau-Rauch” condition. The rate $\tau(\omega)$
decays exponentially in timeas soon as ωsatisfies a geometrical condition known as the “Bardos-Lebeau-Rauch” condition. The rate $\tau(\omega)$ 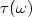 of this decay satisfies $\tau(\omega)= 2 \min( -\mu(\omega),g(\omega))$
of this decay satisfies $\tau(\omega)= 2 \min( -\mu(\omega),g(\omega))$ 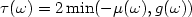 (see Lebeau [Math.Phys. Stud.19 (1996) 73–109]). Here $\mu(\omega)$
(see Lebeau [Math.Phys. Stud.19 (1996) 73–109]). Here $\mu(\omega)$ 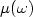 denotes the spectral abscissa of thedamped wave equation operator and $g(\omega)$
denotes the spectral abscissa of thedamped wave equation operator and $g(\omega)$ 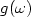 is a number called the geometrical quantity of ω and defined as follows.A ray in Ω is the trajectory generated by thefree motion of a mass-point in Ω subject to elastic reflections on theboundary. These reflections obey the law of geometrical optics.The geometrical quantity $g(\omega)$
is a number called the geometrical quantity of ω and defined as follows.A ray in Ω is the trajectory generated by thefree motion of a mass-point in Ω subject to elastic reflections on theboundary. These reflections obey the law of geometrical optics.The geometrical quantity $g(\omega)$ 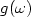 is then defined as the upper limit (large timeasymptotics) of the average trajectory length. We give here an algorithm to compute explicitly $g(\omega)$
is then defined as the upper limit (large timeasymptotics) of the average trajectory length. We give here an algorithm to compute explicitly $g(\omega)$ 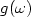 when ωis a finite union of squares.
when ωis a finite union of squares.