Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T10:29:22.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric constraints on the domain for a class of minimum problems

Published online by Cambridge University Press:  15 September 2003

Graziano Crasta  and
Annalisa Malusa
Graziano Crasta
Affiliation:
Dip. di Matematica, P.le Aldo Moro 2, 00185 Roma, Italy; [email protected]. [email protected].
Annalisa Malusa
Affiliation:
Dip. di Matematica, P.le Aldo Moro 2, 00185 Roma, Italy; [email protected]. [email protected].
Get access

Abstract

We consider minimization problems of the form ${\rm min}_{u\in \varphi +W^{1,1}_0(\Omega)}\int_\Omega [f(Du(x))-u(x)]\, {\rm d}x$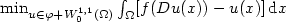 where $\Omega\subseteq \mathbb{R}^N$ 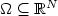is a bounded convex open set, and the Borel function $f\colon \mathbb{R}^N \to [0, +\infty]$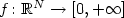 is assumed to be neither convex nor coercive. Under suitable assumptions involving the geometry of Ω and the zero level set of f, we prove that the viscosity solution of a related Hamilton–Jacobi equation provides a minimizer for the integral functional.

Keywords

Calculus of Variationsexistencenon-convex problemsnon-coercive problemsviscosity solutions.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 9 , January 2003 , pp. 125 - 133
Copyright
© EDP Sciences, SMAI, 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M. Bardi and I. Capuzzo Dolcetta, Optimal control and viscosity solutions of Hamilton-Jacobi-Bellman equations. Birkhäuser, Boston (1997).
G. Barles, Solutions de viscosité des équations de Hamilton-Jacobi. Springer Verlag, Berlin (1994).
Bauman, P. and Phillips, D., A non-convex variational problem related to change of phase. Appl. Math. Optim. 21 (1990) 113-138. CrossRef
Cardaliaguet, P., Dacorogna, B., Gangbo, W. and Georgy, N., Geometric restrictions for the existence of viscosity solutions. Ann. Inst. H. Poincaré Anal. Non Linéaire 16 (1999) 189-220. CrossRef
P. Celada, Some scalar and vectorial problems in the Calculus of Variations, Ph.D. Thesis. SISSA, Trieste (1997).
Celada, P. and Cellina, A., Existence and non existence of solutions to a variational problem on a square. Houston J. Math. 24 (1998) 345-375.
Celada, P., Perrotta, S. and Treu, G., Existence of solutions for a class of non convex minimum problems. Math. Z. 228 (1998) 177-199. CrossRef
Cellina, A., Minimizing a functional depending on ∇u and on u. Ann. Inst. H. Poincaré Anal. Non Linéaire 14 (1997) 339-352. CrossRef
Cellina, A. and Perrotta, S., On minima of radially symmetric functionals of the gradient. Nonlinear Anal. 23 (1994) 239-249. CrossRef
Crasta, G., On the minimum problem for a class of non-coercive non-convex variational problems. SIAM J. Control Optim. 38 (1999) 237-253. CrossRef
Crasta, G., Existence, uniqueness and qualitative properties of minima to radially symmetric non-coercive non-convex variational problems. Math. Z. 235 (2000) 569-589. CrossRef
Crasta, G. and Malusa, A., Euler-Lagrange inclusions and existence of minimizers for a class of non-coercive variational problems. J. Convex Anal. 7 (2000) 167-181.
Crasta, G. and Malusa, A., Non-convex minimization problems for functionals defined on vector valued functions. J. Math. Anal. Appl. 254 (2001) 538-557. CrossRef
Dacorogna, B. and Marcellini, P., Existence of minimizers for non-quasiconvex integrals. Arch. Rational Mech. Anal. 131 (1995) 359-399. CrossRef
Kawohl, B., Stara, J. and Wittum, G., Analysis and numerical studies of a problem of shape design. Arch. Rational Mech. Anal. 114 (1991) 349-363. CrossRef
Kohn, R. and Strang, G., Optimal design and relaxation of variational problems, I, II and III. Comm. Pure Appl. Math. 39 (1976) 113-137, 139-182, 353-377. CrossRef
P.L. Lions, Generalized solutions of Hamilton-Jacobi equations. Pitman, London, Pitman Res. Notes Math. Ser. 69 (1982).
E. Mascolo and R. Schianchi, Existence theorems for nonconvex problems J. Math. Pures Appl. 62 (1983) 349-359.
R.T. Rockafellar, Convex Analysis. Princeton Univ. Press, Princeton (1970).
Treu, G., An existence result for a class of non convex problems of the Calculus of Variations. J. Convex Anal. 5 (1998) 31-44.
Vornicescu, M., A variational problem on subsets of $\mathbb{R}^n$ . Proc. Roy. Soc. Edinburg Sect. A 127 (1997) 1089-1101. CrossRef