Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T22:34:22.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Gamma-convergence results for phase-field approximations of the 2D-Euler Elastica Functional

Published online by Cambridge University Press:  03 June 2013

Luca Mugnai
Luca Mugnai*
Affiliation:
Max Planck Institute for Mathematics in the Sciences, Inselstr. 22, 04103 Leipzig, Germany. [email protected]
Get access

Abstract

We establish some new results about the Γ-limit, with respect to the L1-topology, of two different (but related) phase-field approximations \hbox{$\{\mathcal E_\eps\}_\eps,\,\{\widetilde{\mathcalE}_\eps\}_\eps$}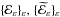{ℰε}ε, {􏽥ℰε}ε of the so-called Euler’s Elastica Bending Energy for curves in the plane. In particular we characterize the Γ-limit as ε → 0 of ℰε, and show that in general the Γ-limits of ℰε and \hbox{$\widetilde{\mathcal E}_\eps$}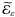􏽥ℰε do not coincide on indicator functions of sets with non-smooth boundary. More precisely we show that the domain of the Γ-limit of \hbox{$\widetilde{\mathcal E}_\eps$}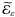􏽥ℰε strictly contains the domain of the Γ-limit of ℰε.

Keywords

Γ-convergencerelaxationsingular perturbationgeometric measure theory
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 19 , Issue 3 , July 2013 , pp. 740 - 753
Copyright
© EDP Sciences, SMAI, 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellettini, G., Dal Maso, G. and Paolini, M., Semicontinuity and relaxation properties of a curvature depending functional in 2d. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 20 (1993) 247–297. Google Scholar
Bellettini, G. and Mugnai, L., A varifolds representation of the relaxed elastica functional. J. Convex Anal. 14 (2007) 543–564. Google Scholar
Bellettini, G. and Mugnai, L., Approximation of Helfrich’s functional via diffuse interfaces. SIAM J. Math. Anal. 42 (2010) 2402–2433. Google Scholar
G. Bellettini and M. Paolini, Approssimazione variazionale di funzionali con curvatura. Seminario Analisi Matematica Univ. Bologna (1993).
Braides, A. and March, R., Approximation by Γ-convergence of a curvature-depending functional in visual reconstruction. Commun. Pure Appl. Math. 59 (2006) 71–121. Google Scholar
Cabré, X. and Terra, J., Saddle-shaped solutions of bistable diffusion equations in all of R2m. J. Eur. Math. Soc. 43 (2009) 819–943. Google Scholar
G. Dal Maso, An introduction to Γ-convergence, vol. 8, Progress in Nonlinear Differential Equations and their Applications. Birkhäuser, Boston, MA (1993).
Dang, H., Fife, P. and Peletier, L., Saddle solutions of the bistable diffusion equation. Z. Angew. Math. Phys. 43 (1992) 984–998. Google Scholar
De Giorgi, E., Some remarks on Γ-convergence and least squares method, in Composite media and homogenization theory (Trieste, 1990), MA. Progr. Nonlinear Differ. Eq. Appl. 5 (1991) 135–142. Google Scholar
Dondl, P., Mugnai, L. and Röger, M., Confined elastic curves. SIAM J. Appl. Math. 71 (2011) 2205–2226. Google Scholar
Du, Q., Liu, C., Ryham, R. and Wang, X., A phase field formulation of the Willmore problem. Nonlinearity 18 (2005) 1249–1267. Google Scholar
Du, Q., Liu, C. and Wang, X., A phase field approach in the numerical study of the elastic bending energy for vesicle membranes. J. Comput. Phys. 198 (2004) 450–468. Google Scholar
Hutchinson, J., C 1, α-multiple function regularity and tangent cone behavior for varifolds with second fundamental form in L p, in Geometric measure theory and the calculus of variations (Arcata, Calif., 1984). Proc. Sympos. Pure Math. Amer. Math. Soc. 44 (1984) 281–306. Google Scholar
Hutchinson, J., Second fundamental form for varifolds and the existence of surfaces minimising curvature. Indiana Univ. Math. J. 35 (1986) 281–306. Google Scholar
Lowengrub, J.S., Rätz, A. and Voigt, A., Phase-field modeling of the dynamics of multicomponent vesicles: spinodal decomposition, coarsening, budding, and fission. Phys. Rev. E 79 (2009) 82C99–92C10. Google ScholarPubMed
Modica, L. and Mortola, S., Un esempio di Γ − -convergenza. Boll. Un. Mat. Ital. B 14 (1977) 285–299. Google Scholar
Nagase, Y. and Tonegawa, Y., A singular perturbation problem with integral curvature bound. Hiroshima Math. Journal 37 (2007) 455–489. Google Scholar
Röger, M. and Schätzle, R.. On a modified conjecture of De Giorgi. Math. Z. 254 (2006) 675–714. Google Scholar
L. Simon, Proceedings of the Centre for Mathematical Analysis, Australian National University. Centre for Math. Anal., Lectures on Geometric Measure Theory, vol. 3. Australian National Univ., Canberra (1984).