Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T06:02:10.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of solutions for a semilinear ellipticsystem

Published online by Cambridge University Press:  15 February 2013

Mohamed Benrhouma
Mohamed Benrhouma*
Affiliation:
Mathematics Department, Sciences Faculty of Monastir, 5019 Monastir, Tunisia. [email protected]
Get access

Abstract

This paper deals with the existence of solutions to the following system: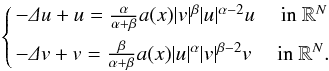

$$\left\{\begin{array}{l} -\Deltau+u=\frac{\alpha}{\alpha+\beta}a(x)|v|^{\beta} |u|^{\alpha-2}u\quad\mbox{ in}\mathbb{R}^N\\ [0.2cm] -\Delta v+v=\frac{\beta}{\alpha+\beta}a(x)|u|^{\alpha}|v|^{\beta-2}v\quad\mbox{ in }\mathbb{R}^N. \end{array}\right.$$−Δu+u=αα+βa(x)|v|β|u|α−2u inRN−Δv+v=βα+βa(x)|u|α|v|β−2v inRN.

With the help of the Nehari manifold and the linking theorem, we prove the existence ofat least two nontrivial solutions. One of them is positive. Our main tools are theconcentration-compactness principle and the Ekeland’s variational principle.

Keywords

Semilinear elliptic systemsNehari manifoldconcentration-compactness principlevariational methods
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 19 , Issue 2 , April 2013 , pp. 574 - 586
Copyright
© EDP Sciences, SMAI, 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

An, Y., Uniqueness of positive solutions for a class of elliptic systems. J. Math. Anal. Appl. 322 (2006) 1071–1082. Google Scholar
Benci, V., Some critical point theorems and applications. Commun. Pure Appl. Math. 33 (1980) 147–172. Google Scholar
Busca, J. and Sirakov, B., Symmetry results for semilinear elliptic systems in the whole space. J. Differ. Equ. 163 (2000) 41–56. Google Scholar
Chen, K.-J., Multiplicity for strongly indefinite semilinear elliptic system. Nonlinear Anal. 72 (2010) 806–821. Google Scholar
Clement, P., Figuereido, D.G. and Mitidieri, E., Positive solutions of semilinear elliptic systems. Commun. Partial Differ. Equ. 17 (1992) 923–940. Google Scholar
Costa, D.G., On a class of elliptic systems in RN. Electron. J. Differ. Equ. 7 (1994) 1–14. Google Scholar
Cui, R., Wang, Y. and Shi, J., Uniqueness of the positive solution for a class of semilinear elliptic systems. Nonlinear Anal. 67 (2007) 1710–1714. Google Scholar
Dalmasso, R., Existence and uniqueness of positive solutions of semilinear elliptic systems. Nonlinear Anal. 39 (2000) 559–568. Google Scholar
De Finueirdo, D.G. and Yang, J.F., Decay, symmetry and existence of solutions of semilinear elliptic systems. Nonlinear Anal. 33 (1998) 211–234. Google Scholar
Ekeland, I., On the variational principle. J. Math. Anal. Appl. 47 (1974) 324–353. Google Scholar
Gongbao, L. and Chunhua, W., The existence of nontrivial solutions to a semilinear elliptic system on RN without the Ambrosetti-Rabinowitz condition. Acta Math. Sci. B 30 (2010) 1917–1936. Google Scholar
Hai, D.D., Uniqueness of positive solutions for semilinear elliptic systems. J. Math. Anal. Appl. 313 (2006) 761–767. Google Scholar
Lair, A.V. and Wood, A.W., Existence of entire large positive solutions of semilinear elliptic systems, J. Differ. Equ. 164 (2000) 380–394. Google Scholar
Li, G.B. and Yang, J.F., Asymptotically linear elliptic systems. Commun. Partial Differ. Equ. 29 (2004) 925–954. Google Scholar
Lions, P.L., the concentration-compactness principle in the calculus of variations. The locally compact case, part 1. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 1 (1984) 109–145. Google Scholar
Lions, P.L., the concentration-compactness principle in the calculus of variations. The locally compact case, part 2. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 2 (1984) 223–283. Google Scholar
Nehari, Z., On a class of nonlinear second-order differential equations. Trans. Amer. Math. Soc. 95 (1960) 101–123. Google Scholar
Ni, W.-M., Some minimax principles and their applications in nonlinear elliptic equations. J. Anal. Math. 37 (1980) 248–275. Google Scholar
Rabinowitz, P.H., Some critical point theorems and applications to semilinear elliptic partial differential equations. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 5 (1978) 215–223. Google Scholar
Serrin, J. and Zou, H., Nonexistence of positive solutions of Lane-Emden systems. Differ. Integral Equ. 9 (1996) 635–653. Google Scholar
Wu, T.-F., The Nehari manifold for a semilinear elliptic system involving sign-changing weight functions. Nonlinear Anal. 68 (2008) 1733–1745. Google Scholar