Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T10:34:49.081Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution equations in discrete and continuous time for nonexpansive operators in Banach spaces

Published online by Cambridge University Press:  31 July 2009

Guillaume Vigeral
Guillaume Vigeral*
Affiliation:
Équipe Combinatoire et Optimisation, CNRS FRE3232, Université Pierre et Marie Curie, Paris 6, UFR 929, 175 rue du Chevaleret, 75013 Paris, France. [email protected]
Get access

Abstract

We consider some discrete and continuous dynamics in a Banach spaceinvolving a non expansive operator J and a corresponding family ofstrictly contracting operators Φ (λ, x): = λJ( $\frac{1-\lambda}{\lambda}$ 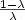x) for λ ∈ ] 0,1] . Our motivationcomes from the study of two-player zero-sum repeated games, wherethe value of the n-stage game (resp. the value of theλ-discounted game) satisfies the relationv n = Φ( $\frac{1}{n}$ 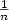, $v_{n-1}$ 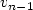) (resp.  $v_\lambda$ 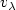= Φ(λ, $v_\lambda$ 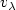)) where J is the Shapleyoperator of the game. We study the evolution equationu'(t) = J(u(t))- u(t) as well as associated Eulerian schemes,establishing a new exponential formula and a Kobayashi-likeinequality for such trajectories. We prove that the solution of thenon-autonomous evolution equationu'(t) = Φ(λ(t), u(t))- u(t) has the same asymptoticbehavior (even when it diverges) as the sequence v n (resp. as thefamily $v_\lambda$ 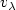) when λ(t) = 1/t (resp. whenλ(t) converges slowly enough to 0).

Keywords

Banach spacesnonexpansive mappingsevolution equationsasymptotic behaviorShapley operator
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 4 , October 2010 , pp. 809 - 832
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Attouch, H. and Cominetti, R., A dynamical approach to convex minimization coupling approximation with the steepest descent method. J. Differ. Equ. 128 (1996) 269–275. CrossRef
R.J. Aumann and M. Maschler with the collaboration of R.E. Stearns, Repeated Games with Incomplete Information. MIT Press (1995).
V. Barbu, Nonlinear Semigroups and Differential Equations in Banach Spaces. Noordhoff International Publishing (1976).
Bewley, T. and Kohlberg, E., The asymptotic theory of stochastic games. Math. Oper. Res. 1 (1976) 197–208. CrossRef
Bewley, T. and Kohlberg, E., The asymptotic solution of a recursion equation occurring in stochastic games. Math. Oper. Res. 1 (1976) 321–336. CrossRef
H. Brézis, Opérateurs Maximaux Monotones et Semi-Groupes de Contractions dans les Espaces de Hilbert, Mathematical Studies 5. North Holland (1973).
Crandall, M.G. and Liggett, T.M., Generation of semi-groups of nonlinear transformations on general Banach spaces. Amer. J. Math. 93 (1971) 265–298. CrossRef
H. Everett, Recursive Games, in Contributions to the Theory of Games 3, H.W. Kuhn and A.W. Tucker Eds., Princeton University Press (1957) 47–78.
Gaubert, S. and Gunawardena, J., The Perron-Frobenius Theorem for homogeneous, monotone functions. T. Am. Math. Soc. 356 (2004) 4931–4950. CrossRef
Gunawardena, J., From max-plus algebra to nonexpansive maps: a nonlinear theory for discrete event systems. Theor. Comput. Sci. 293 (2003) 141–167. CrossRef
J. Gunawardena and M. Keane, On the existence of cycle times for some nonexpansive maps. Technical Report HPL-BRIMS-95-003 Ed., Hewlett-Packard Labs (1995).
Kato, T., Nonlinear semi-groups and evolution equations. J. Math. Soc. Japan 19 (1967) 508–520. CrossRef
Kobayashi, Y., Difference approximation of Cauchy problems for quasi-dissipative operators and generation of nonlinear semigroups. J. Math Soc. Japan 27 (1975) 640–665. CrossRef
Kohlberg, E., Repeated games with absorbing states. Ann. Stat. 2 (1974) 724–738. CrossRef
Kohlberg, E. and Neyman, A., Asymptotic behavior of nonexpansive mappings in normed linear spaces. Israel J. Math. 38 (1981) 269–275. CrossRef
Lehrer, E. and Sorin, S., A uniform Tauberian theorem in dynamic programming. Math. Oper. Res. 17 (1992) 303–307. CrossRef
Miyadera, I. and Oharu, S., Approximation of semi-groups of nonlinear operators. Tôhoku Math. J. 22 (1970) 24–47. CrossRef
Moreau, J.-J., Propriétés des applications “prox”. C. R. Acad. Sci. Paris 256 (1963) 1069–1071.
A. Neyman, Stochastic games and nonexpansive maps, in Stochastic Games and Applications, A. Neyman and S. Sorin Eds., Kluwer Academic Publishers (2003) 397–415.
A. Neyman and S. Sorin, Repeated games with public uncertain duration process. (Submitted).
Reich, S., Asymptotic behavior of semigroups of nonlinear contractions in Banach spaces. J. Math. Anal. Appl. 53 (1976) 277–290. CrossRef
Renault, J., The Value of Markov Chain Games with Lack of Information on One Side. Math. Oper. Res. 31 (2006) 490–512. CrossRef
R. Rockafellar, Convex Analysis. Princeton University Press (1970).
Rosenberg, D. and Sorin, S., An operator approach to zero-sum repeated games. Israel J. Math. 121 (2001) 221–246. CrossRef
S. Sorin, A First Course on Zero-Sum Repeated Games. Springer (2002).
Sorin, S., Asymptotic properties of monotonic nonexpansive mappings. Discrete Events Dynamical Systems 14 (2004) 109–122. CrossRef
W. Walter, Differential and Integral Inequalities. Springer-Verlag (1970).