Article contents
Equivalent formulation and numerical analysis of a fire confinement problem
Published online by Cambridge University Press: 11 August 2009
Abstract
We consider a class of variationalproblems for differential inclusions, related to thecontrol of wild fires. The area burned by the fire at time t> 0is modelled as the reachable set fora differential inclusion $\dot x$ 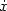 ∈F(x), starting froman initial set R 0. To block the fire, a barrier can be constructedprogressively in time. For each t> 0, the portion of the wall constructedwithin time t is described by a rectifiable setγ(t) ⊂ $\mathbb{R}^2$
∈F(x), starting froman initial set R 0. To block the fire, a barrier can be constructedprogressively in time. For each t> 0, the portion of the wall constructedwithin time t is described by a rectifiable setγ(t) ⊂ $\mathbb{R}^2$ 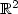 . In this paperwe show that the searchfor blocking strategies and for optimal strategies can be reduced toa problem involving one single admissible rectifiable set Γ⊂ $\mathbb{R}^2$
. In this paperwe show that the searchfor blocking strategies and for optimal strategies can be reduced toa problem involving one single admissible rectifiable set Γ⊂ $\mathbb{R}^2$ 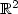 ,rather than the multifunction t $\mapsto$
,rather than the multifunction t $\mapsto$  γ(t) ⊂ $\mathbb{R}^2$
γ(t) ⊂ $\mathbb{R}^2$ 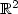 .Relying on this result, we then developa numerical algorithm for the computation ofoptimal strategies, minimizing the total area burned by the fire.
.Relying on this result, we then developa numerical algorithm for the computation ofoptimal strategies, minimizing the total area burned by the fire.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 4 , October 2010 , pp. 974 - 1001
- Copyright
- © EDP Sciences, SMAI, 2009
References
- 10
- Cited by


