Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T12:39:51.007Z Has data issue: false hasContentIssue false
  • English
  • Français

The dynamical Lame system: regularity of solutions, boundary controllability and boundary data continuation

Published online by Cambridge University Press:  15 August 2002

M. I. Belishev  and
I. Lasiecka
M. I. Belishev
Affiliation:
Saint-Petersburg Department of the Steklov Mathematical Institute (POMI), Fontanka 27, St. Petersburg 191011, Russia; [email protected].
I. Lasiecka
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22901, USA; [email protected].
Get access

Abstract

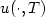The boundary control problem for the dynamical Lame system(isotropic elasticity model) is considered. The continuity ofthe “input → state" map in L 2-norms is established. A structure of thereachable sets for arbitrary T>0 is studied.In general case, only the first component $u(\cdot ,T)$ of thecomplete state $\{ u(\cdot ,T),u_t(\cdot ,T)\}$ 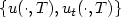may be controlled, an approximate controllability occurring inthe subdomain filled with the shear (slow) waves. The controllability results are applied to the problem of the boundarydata continuation. If T 0 exceeds the time neededfor shear waves to fill the entire domain, then the responseoperator (“input → output" map) $R^{2T_0}$ 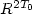uniquely determinesRT for any T>0. A procedure recovering R ∞via $R^{2T_0}$ 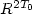is also described.

Keywords

Isotropic elasticitydynamical Lame systemregularity of solutionsstructure of sets reachable from the boundary in a short timeboundary controllability.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 8: A tribute to JL Lions , 2002 , pp. 143 - 167
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avdonin, S.A., Belishev, M.I. and Ivanov, S.A., The controllability in the filled domain for the higher dimensional wave equation with the singular boundary control. Zapiski Nauch. Semin. POMI 210 (1994) 7-21. English translation: J. Math. Sci. 83 (1997).
Bardos, C., Masrour, T. and Tatout, F., Observation and control of Elastic waves. IMA Vol. in Math. Appl. Singularities and Oscillations 191 (1996) 1-16.
Belishev, M.I., Canonical model of a dynamical system with boundary control in the inverse problem of heat conductivity. St-Petersburg Math. J. 7 (1996) 869-890.
Belishev, M.I., Boundary control in reconstruction of manifolds and metrics (the BC-method). Inv. Prob. 13 (1997) R1-R45. CrossRef
Belishev, M.I., On relations between spectral and dynamical inverse data. J. Inv. Ill-Posed Problems 9 (2001) 547-565. CrossRef
Belishev, M.I., Dynamical systems with boundary control: Models and characterization of inverse data. Inv. Prob. 17 (2001) 659-682. CrossRef
Belishev, M.I. and Glasman, A.K., Boundary control of the Maxwell dynamical system: Lack of controllability by topological reasons. ESAIM: COCV 5 (2000) 207-217. CrossRef
M.S. Birman and M.Z. Solomjak, Spectral Theory of Self-Adjoint Operators in Hilbert Space. D. Reidel Publishing Comp. (1987).
M. Eller, V. Isakov, G. Nakamura and D. Tataru, Uniqueness and stability in the Cauchy problem for maxwell's and elasticity systems, in Nonlinear PDE, College de France Seminar J.-L. Lions. Series in Appl. Math. 7 (2002).
V. Isakov, Inverse Problems for Partial Differential Equations. Springer-Verlag, New-York (1998).
John, F., On linear partial differential equations with analytic coefficients. Unique continuation of data. Comm. Pure Appl. Math. 2 (1948) 209-253. CrossRef
Krein, M.G., On the problem of extension of the Hermitian positive continuous functions. Dokl. Akad. Nauk SSSR 26 (1940) 17-21.
Lasiecka, I., Lions, J.-L. and Triggiani, R., Non homogeneous boundary value problems for second order hyperbolic operators. J. Math. Pures Appl. 65 (1986) 149-192.
Lasiecka, I., Uniform decay rates for full von Karman system of dynamic thermoelasticity with free boundary conditions and partial boundary dissipation. Comm. on PDE's 24 (1999) 1801-1849. CrossRef
Lasiecka, I. and Triggiani, R., A cosine operator approach to modeling L 2 boundary input hyperbolic equations. Appl. Math. Optim. 7 (1981) 35-93. CrossRef
Lasiecka, I. and Triggiani, R., A lifting theorem for the time regularity of solutions to abstract equations with unbounded operators and applications to hyperbolic equations. Proc. AMS 104 (1988) 745-755. CrossRef
R. Leis, Initial boundary value problems in Mathematical Physics. John Wiley - Sons LTD and B.G. Teubner, Stuttgart (1986).
Russell, D.L., Boundary value control theory of the higher dimensional wave equation. SIAM J. Control 9 (1971) 29-42. CrossRef
M. Sova, Cosine Operator Functions. Rozprawy matematyczne XLIX (1966).
Tataru, D., Unique continuation for solutions of PDE's: Between Hormander's and Holmgren theorem. Comm. PDE 20 (1995) 855-894.
Weck, N., Aussenraumaufgaben in der Theorie station ärer Schwingungen inhomogener elastischer Körper. Math. Z. 111 (1969) 387-398. CrossRef