Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T10:27:07.844Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity of solutions of a nonlinear ellipticequation

Published online by Cambridge University Press:  16 January 2012

Pierre Bousquet
Pierre Bousquet*
Affiliation:
Université Aix-Marseille 1, LATP UMR6632 3 place Victor Hugo, 13331 Marseille Cedex 3, France. [email protected]
Get access

Abstract

We consider a nonlinear elliptic equation of the formdiv [a(∇u)] + F[u] = 0on a domain Ω, subject to a Dirichlet boundary conditiontru = φ. We do not assume that the higher order terma satisfies growth conditions from above. We prove the existence ofcontinuous solutions either when Ω is convex and φ satisfies a one-sidedbounded slope condition, or when a is radial:\hbox{$a(\xi)=\fr{l(|\xi|)}{|\xi|} \xi$}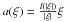a(ξ)=l(|ξ|)|ξ|ξ for some increasingl:ℝ+ → ℝ+.

Keywords

Nonlinear elliptic equationscontinuity of solutionslower bounded slope conditionLavrentiev phenomenon
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 19 , Issue 1 , January 2013 , pp. 1 - 19
Copyright
© EDP Sciences, SMAI, 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bousquet, P., The lower bounded slope condition. J. Convex Anal. 1 (2007) 119 − 136. Google Scholar
Bousquet, P., Local Lipschitz continuity of solutions of non-linear elliptic differential-functional equations. ESAIM Control Optim. Calc. Var. 13 (2007) 707 − 716. Google Scholar
Bousquet, P., Continuity of solutions of a problem in the calculus of variations. Calc. Var. Partial Differential Equations 41 (2011) 413 − 433. Google Scholar
Clarke, F., Continuity of solutions to a basic problem in the calculus of variations. Ann. Scvola Norm. Super. Pisa Cl. Sci. (5) 4 (2005) 511 − 530. Google Scholar
Degiovanni, M. and Marzocchi, M., On the Euler-Lagrange equation for functionals of the calculus of variations without upper growth conditions. SIAM J. Control Optim. 48 (2009) 2857 − 2870. Google Scholar
D. Gilbarg and N.S. Trudinger, Elliptic partial differential equations of second order. Classics in Mathematics, Springer-Verlag, Berlin (2001) Reprint of the 1998 edition.
Hartman, P., On the bounded slope condition. Pac. J. Math. 18 (1966) 495 − 511. Google Scholar
Hartman, P. and Stampacchia, G., On some non-linear elliptic differential-functional equations. Acta Math. 115 (1966) 271 − 310. Google Scholar
O.A. Ladyzhenskaya and N.N. Uraltseva, Linear and quasilinear elliptic equations. Academic Press, New York (1968).
C.B. Morrey, Multiple integrals in the calculus of variations. Springer-Verlag, New York (1966).