Aubry sets and the differentiability of the minimal average action in codimension one

Abstract

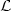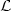Let ${\cal L}$ (x,u,∇ u) be a Lagrangian periodic of period 1 in x ₁,...,x _n ,u. We shall study the non self intersectingfunctions u: R ⁿ ${\to}$ R minimizing ${\cal L}$ ; non self intersecting means that, if u(x ₀ + k) + j = u(x ₀) for some x ₀∈R ⁿ and (k , j) ∈Z ⁿ × Z, then u(x) = u(x + k) + j $\;\forall$ 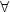x. Moser has shown that each of these functions is at finite distance from a plane u = ρ $\cdot$ x and thus has an average slope ρ; moreover, Senn has proven that it is possible to define the average action of u, which is usually called $\beta(\rho)$ 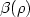since it only depends on the slope of u.Aubry and Senn have noticed a connection between $\beta(\rho)$ 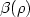and the theory of crystals in ${\bf R}^{n+1}$ 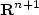, interpreting $\beta(\rho)$ 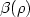as the energy per area of a crystal face normal to $(-\rho,1)$ 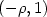. The polar of β is usually called -α; Senn has shown that α is C ¹ and that the dimension of the flat of α which contains c depends only on the “rational space” of $\alpha^\prime$ 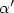(c). We prove a similar result for the faces (or the faces of the faces, etc.) of the flats of α: they are C ¹ and their dimension depends only on the rational space of their normals.