Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Maingé, Paul-Emile
2013.
First-Order Continuous Newton-like Systems for Monotone Inclusions.
SIAM Journal on Control and Optimization,
Vol. 51,
Issue. 2,
p.
1615.
Wu, Yuhu
and
Xue, Xiaoping
2013.
ASYMPTOTICS FOR A DISSIPATIVE DYNAMICAL SYSTEM WITH LINEAR AND GRADIENT-DRIVEN DAMPING.
Mathematical Modelling and Analysis,
Vol. 18,
Issue. 5,
p.
654.
Abbas, Boushra
and
Attouch, Hédy
2015.
Dynamical systems and forward–backward algorithms associated with the sum of a convex subdifferential and a monotone cocoercive operator.
Optimization,
Vol. 64,
Issue. 10,
p.
2223.
Boţ, Radu Ioan
and
Csetnek, Ernö Robert
2016.
Second Order Forward-Backward Dynamical Systems For Monotone Inclusion Problems.
SIAM Journal on Control and Optimization,
Vol. 54,
Issue. 3,
p.
1423.
Boţ, Radu Ioan
and
Csetnek, Ernö Robert
2017.
Second-order dynamical systems associated to variational inequalities.
Applicable Analysis,
Vol. 96,
Issue. 5,
p.
799.
Boţ, Radu Ioan
and
Csetnek, Ernö Robert
2017.
Levenberg-Marquardt Dynamics Associated to Variational Inequalities.
Set-Valued and Variational Analysis,
Vol. 25,
Issue. 3,
p.
569.
Attouch, Hedy
and
Cabot, Alexandre
2018.
Convergence of damped inertial dynamics governed by regularized maximally monotone operators.
Journal of Differential Equations,
Vol. 264,
Issue. 12,
p.
7138.
Ibrahim, Adrianto Ravi
and
Hayakawa, Tomohisa
2018.
Nash Equilibrium Seeking with Second-Order Dynamic Agents.
p.
2514.
Boţ, Radu Ioan
and
Csetnek, Ernö Robert
2018.
Convergence rates for forward–backward dynamical systems associated with strongly monotone inclusions.
Journal of Mathematical Analysis and Applications,
Vol. 457,
Issue. 2,
p.
1135.
Attouch, Hedy
and
Peypouquet, Juan
2019.
Convergence of inertial dynamics and proximal algorithms governed by maximally monotone operators.
Mathematical Programming,
Vol. 174,
Issue. 1-2,
p.
391.
Rouhani, Behzad Djafari
and
Piranfar, Mohsen Rahimi
2019.
Nonhomogeneous nonlinear oscillator with damping: asymptotic analysis in continuous and discrete time.
Demonstratio Mathematica,
Vol. 52,
Issue. 1,
p.
274.
Boţ, Radu Ioan
and
Csetnek, Ernö Robert
2019.
A second-order dynamical system with Hessian-driven damping and penalty term associated to variational inequalities.
Optimization,
Vol. 68,
Issue. 7,
p.
1265.
Attouch, Hedy
and
Cabot, Alexandre
2019.
Convergence of a Relaxed Inertial Forward–Backward Algorithm for Structured Monotone Inclusions.
Applied Mathematics & Optimization,
Vol. 80,
Issue. 3,
p.
547.
Attouch, Hedy
and
László, Szilárd Csaba
2020.
Newton-like Inertial Dynamics and Proximal Algorithms Governed by Maximally Monotone Operators.
SIAM Journal on Optimization,
Vol. 30,
Issue. 4,
p.
3252.
Attouch, Hedy
and
Cabot, Alexandre
2020.
Convergence of a relaxed inertial proximal algorithm for maximally monotone operators.
Mathematical Programming,
Vol. 184,
Issue. 1-2,
p.
243.
Liu, Liya
Qin, Xiaolong
and
Yao, Jen-Chih
2020.
A Hybrid Forward–Backward Algorithm and Its Optimization Application.
Mathematics,
Vol. 8,
Issue. 3,
p.
447.
Adly, Samir
Attouch, Hedy
and
Vo, Van Nam
2021.
Asymptotic behavior of Newton-like inertial dynamics involving the sum of potential and nonpotential terms.
Fixed Point Theory and Algorithms for Sciences and Engineering,
Vol. 2021,
Issue. 1,
Attouch, Hedy
and
László, Szilárd Csaba
2021.
Continuous Newton-like Inertial Dynamics for Monotone Inclusions.
Set-Valued and Variational Analysis,
Vol. 29,
Issue. 3,
p.
555.
Adly, Samir
Attouch, Hedy
and
Vo, Van Nam
2022.
Newton-Type Inertial Algorithms for Solving Monotone Equations Governed by Sums of Potential and Nonpotential Operators.
Applied Mathematics & Optimization,
Vol. 85,
Issue. 3,
Djafari Rouhani, B.
Khatibzadeh, H.
Rahimi Piranfar, M.
and
Rooin, J.
2022.
Asymptotic behaviour of a dynamical system governed by non-monotone potential and non-potential operators.
Optimization,
Vol. 71,
Issue. 9,
p.
2703.
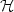 , we investigate the asymptotic behavior, as time t goes to infinity, of trajectories of second-order evolutionequations
, we investigate the asymptotic behavior, as time t goes to infinity, of trajectories of second-order evolutionequations 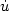 (t) + ∇ϕ(u(t)) + A(u(t)) = 0,
(t) + ∇ϕ(u(t)) + A(u(t)) = 0, 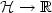 , A : ${\cal H}\to {\cal H}$
, A : ${\cal H}\to {\cal H}$ is a maximal monotone operator which is assumed to beλ-cocoercive, and γ > 0 is a damping parameter.Potential and non-potential effects are associated respectively to∇ϕ and A. Under condition λγ2 > 1, it is proved that each trajectory asymptotically weaklyconverges to a zero of ∇ϕ + A. This condition, whichonly involves the non-potential operator and the dampingparameter, is sharp and consistent with time rescaling. Passingfrom weak to strong convergence of the trajectories is obtained byintroducing an asymptotically vanishing Tikhonov-like regularizingterm. As special cases, we recover the asymptotic analysis of theheavy ball with friction dynamic attached to a convex potential, thesecond-order gradient-projection dynamic, and the second-orderdynamic governed by the Yosida approximation of a general maximalmonotone operator. The breadth and flexibility of the proposed framework is illustrated through applications in the areas of constrained optimization,dynamical approach to Nash equilibria for noncooperative games, and asymptotic stabilization in the case of a continuum of equilibria.
is a maximal monotone operator which is assumed to beλ-cocoercive, and γ > 0 is a damping parameter.Potential and non-potential effects are associated respectively to∇ϕ and A. Under condition λγ2 > 1, it is proved that each trajectory asymptotically weaklyconverges to a zero of ∇ϕ + A. This condition, whichonly involves the non-potential operator and the dampingparameter, is sharp and consistent with time rescaling. Passingfrom weak to strong convergence of the trajectories is obtained byintroducing an asymptotically vanishing Tikhonov-like regularizingterm. As special cases, we recover the asymptotic analysis of theheavy ball with friction dynamic attached to a convex potential, thesecond-order gradient-projection dynamic, and the second-orderdynamic governed by the Yosida approximation of a general maximalmonotone operator. The breadth and flexibility of the proposed framework is illustrated through applications in the areas of constrained optimization,dynamical approach to Nash equilibria for noncooperative games, and asymptotic stabilization in the case of a continuum of equilibria.